Bondi k calculus

History

The k-calculus method had previously been used by E. A. Milne in 1935. Milne used the letter s to denote a constant Doppler factor, but also considered a more general case involving non-inertial motion (and therefore a varying Doppler factor). Bondi used the letter k instead of s and simplified the presentation (for constant k only), and introduced the name "k-calculus".

Bondi's k-factor

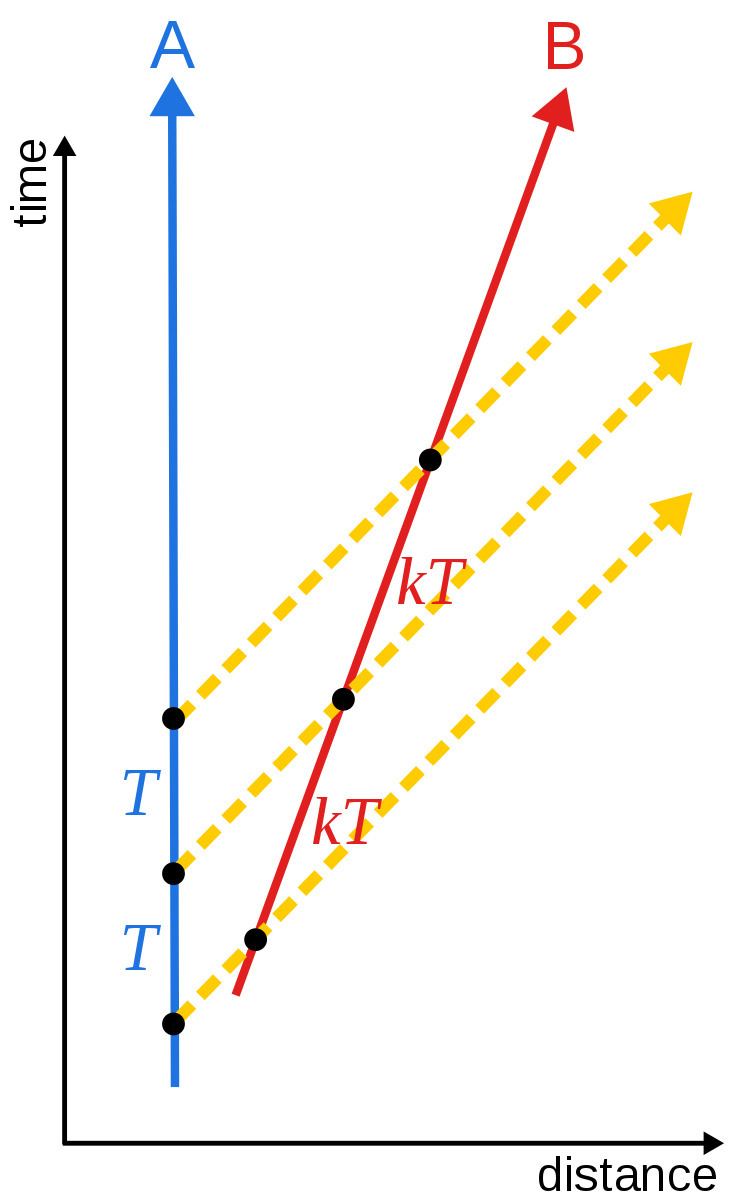
Consider two inertial observers, Alice and Bob, moving directly away from each other at constant relative velocity. Alice sends a flash of blue light towards Bob once every T seconds, as measured by her own clock. Because Alice and Bob are separated by a distance, there is a delay between Alice sending a flash and Bob receiving a flash. Furthermore the separation distance is steadily increasing at a constant rate, so the delay keeps on increasing. This means that the time interval between Bob receiving the flashes, as measured by his clock, is greater than T seconds, say k T seconds for some constant k > 1 . (If Alice and Bob were, instead, moving directly towards each other, a similar argument would apply, but in that case k < 1 .)

Bondi describes k as “a fundamental ratio”, and other authors have since called it "the Bondi k-factor" or "Bondi's k-factor".

Alice's flashes are transmitted at a frequency of f s = 1 / T Hz, by her clock, and received by Bob at a frequency of f o = 1 / ( k T ) Hz, by her clock. This implies a Doppler factor of f s / f o = k . So Bondi's k-factor is another name for the Doppler factor (when source Alice and observer Bob are moving directly away from or towards each other).

If Alice and Bob were to swap roles, and Bob sent flashes of light to Alice, the Principle of Relativity (Einstein's first postulate) implies that the k-factor from Bob to Alice would be the same value as the k-factor from Alice to Bob, as all inertial observers are equivalent. So the k-factor depends only on the relative speed between the observers and nothing else.  

The reciprocal k-factor

Consider, now, a third inertial observer Dave who is a fixed distance from Alice, and such that Bob lies on the straight line between Alice and Dave. As Alice and Dave are mutually at rest, the delay from Alice to Dave is constant. This means that Dave receives Alice's blue flashes at a rate of once every T seconds, by his clock, the same rate as Alice sends them. In other words, the k-factor from Alice to Dave is equal to one.

Now suppose that whenever Bob receives a blue flash from Alice he immediately sends his own red flash towards Dave, once every k T seconds (by Bob's clock). Einstein's second postulate, that the speed of light is independent of the motion of its source, implies that Alice's blue flash and Bob's red flash both travel at the same speed, neither overtaking the other, and therefore arrive at Dave at the same time. So Dave receives a red flash from Bob every T seconds, by Dave's clock, which were sent by Bob every k T seconds by Bob's clock. This implies that the k-factor from Bob to Dave is 1 / k .

This establishes that the k-factor for observers moving directly apart (red shift) is the reciprocal of the k-factor for observers moving directly towards each other at the same speed (blue shift).  

The twins paradox

Consider, now, a fourth inertial observer Carol who travels from Dave to Alice at exactly the same speed as Bob travels from Alice to Dave. Carol's journey is timed such that she leaves Dave at exactly the same time as Bob arrives. Denote times recorded by Alice's, Bob's and Carol's clocks by t A , t B , t C .

When Bob passes Alice, they both synchronise their clocks to t A = t B = 0 . When Carol passes Bob, she synchronises her clock to Bob's, t C = t B . Finally, as Carol passes Alice, they compare their clocks against each other. In Newtonian physics, the expectation would be that, at the final comparison, Alice's and Carol's clock would agree, t C = t A . It will be shown below that in relativity this is not true. This is a version of the well-known "twins paradox" in which identical twins separate and reunite, only to find that one is now older than the other.

If Alice sends a flash of light at time t A = T towards Bob, then, by the definition of the k-factor, it will be received by Bob at time t B = k T . The flash is timed so that it arrives at Bob just at the moment that Bob meets Carol, so Carol synchronises her clock to read t C = t B = k T .

Also, when Bob and Carol meet, they both simultaneously send flashes to Alice, which are received simultaneously by Alice. Considering, first, Bob's flash, sent at time t B = k T , it must be received by Alice at time t A = k 2 T , using the fact that the k-factor from Alice to Bob is the same as the k-factor from Bob to Alice.

As Bob's outward journey had a duration of k T , by his clock, it follows by symmetry that Carol's return journey over the same distance at the same speed must also have a duration of k T , by her clock, and so when Carol meets Alice, Carol's clock reads t C = 2 k T . The k-factor for this leg of the journey must be the reciprocal 1 / k (as discussed earlier), so, considering Carol's flash towards Alice, a transmission interval of k T corresponds to a reception interval of T . This means that the final time on Alice's clock, when Carol and Alice meet, is t A = ( k 2 + 1 ) T . This is larger than Carol's clock time t C = 2 k T since

provided k ≠ 1 and T > 0 .  

Radar measurements and velocity

In the k-calculus methodology, distances are measured using radar. An observer sends a radar pulse towards a target and receives an echo from it. The radar pulse (which travels at c , the speed of light) travels a total distance, there and back, that is twice the distance to the target, and takes time T 2 − T 1 , where T 1 and T 2 are times recorded by the observer's clock at transmission and reception of the radar pulse. This implies that the distance to the target is

Furthermore, since the speed of light is the same in both directions, the time at which the radar pulse arrives at the target must be, according to the observer, halfway between the transmission and reception times, namely

In the particular case where the radar observer is Alice and the target is Bob (momentarily co-located with Dave) as described previously, by k-calculus we have T 2 = k 2 T 1 , and so

As Alice and Bob were co-located at t A = 0 , x A = 0 , the velocity of Bob relative to Alice is given by

This equation expresses velocity as a function of the Bondi k-factor. It can be solved for k to give k as a function of v :

Velocity composition

Consider three inertial observers Alice, Bob and Ed, arranged in that order and moving at different speeds along the same straight line. In this section, the notation k A B will be used to denote the k-factor from Alice to Bob (and similarly between other pairs of observers).

As before, Alice sends a blue flash towards Bob and Ed every T seconds, by her clock, which Bob receives every k A B T seconds, by Bob's clock, and Ed receives every k A E T seconds, by Ed's clock.

Now suppose that whenever Bob receives a blue flash from Alice he immediately sends his own red flash towards Ed, once every k A B T seconds by Bob's clock, so Ed receives a red flash from Bob every k B E ( k A B T ) seconds, by Ed's clock. Einstein's second postulate, that the speed of light is independent of the motion of its source, implies that Alice's blue flash and Bob's red flash both travel at the same speed, neither overtaking the other, and therefore arrive at Ed at the same time. Therefore, as measured by Ed, the red flash interval k B E ( k A B T ) and the blue flash interval k A E T must be the same. So the rule for combining k-factors is simply multiplication:

Finally, substituting

gives the velocity composition formula

The invariant interval

Using the radar method described previously, inertial observer Alice assigns coordinates ( t A , x A ) to an event by transmitting a radar pulse at time t A − x A / c and receiving its echo at time t A + x A / c , as measured by her clock.

Similarly, inertial observer Bob can assign coordinates ( t B , x B ) to the same event by transmitting a radar pulse at time t B − x B / c and receiving its echo at time t B + x B / c , as measured by his clock. However, as the diagram shows, it is not necessary for Bob to generate his own radar signal, as he can simply take the timings from Alice's signal instead.

Now, applying the k-calculus method to the signal that travels from Alice to Bob

Similarly, applying the k-calculus method to the signal that travels from Bob to Alice

Equating the two expressions for k and rearranging,

This establishes that the quantity c 2 t 2 − x 2 is an invariant: it takes the same value in any inertial coordinate system and is known as the invariant interval.

The Lorentz transformation

The two equations for k in the previous section can be solved as simultaneous equations to obtain:

These equations are the Lorentz transformation expressed in terms of the Bondi k-factor instead of in terms of velocity. By substituting

the more traditional form

is obtained.

Rapidity

Rapidity φ can be defined from the k-factor by

and so

The k-factor version of the Lorentz transform becomes

It follows from the composition rule for k , k A E = k A B k B E , that the composition rule for rapidities is addition: