 | ||
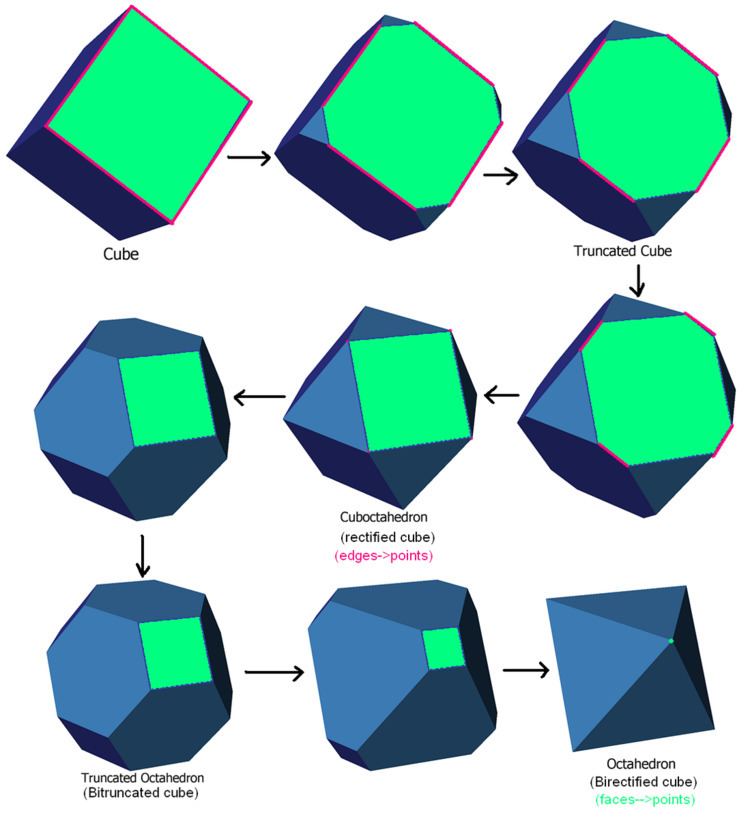
In geometry, a bitruncation is an operation on regular polytopes. It represents a truncation beyond rectification. The original edges are lost completely and the original faces remain as smaller copies of themselves.
Contents
- In regular polyhedra and tilings
- In regular 4 polytopes and honeycombs
- Self dual pqp 4 polytopehoneycombs
- References
Bitruncated regular polytopes can be represented by an extended Schläfli symbol notation t1,2{p,q,...} or 2t{p,q,...}.
In regular polyhedra and tilings
For regular polyhedra, a bitruncated form is the truncated dual. For example, a bitruncated cube is a truncated octahedron.
In regular 4-polytopes and honeycombs
For regular 4-polytope, a bitruncated form is a dual-symmetric operator. A bitruncated 4-polytope is the same as the bitruncated dual.
A regular polytope (or honeycomb) {p, q, r} will have its {p, q} cells bitruncated into truncated {q, p} cells, and the vertices are replaced by truncated {q, r} cells.
Self-dual {p,q,p} 4-polytope/honeycombs
An interesting result of this operation is that self-dual 4-polytope {p,q,p} (and honeycombs) remain cell-transitive after bitruncation. There are 5 such forms corresponding to the five truncated regular polyhedra: t{q,p}. Two are honeycombs on the 3-sphere, one a honeycomb in Euclidean 3-space, and two are honeycombs in hyperbolic 3-space.
