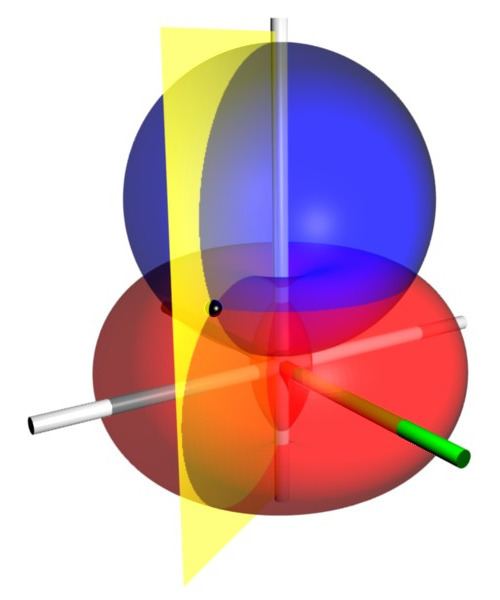
Bispherical coordinates - Alchetron, the free social encyclopedia

Bispherical coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that connects the two foci. Thus, the two foci F 1 and F 2 in bipolar coordinates remain points (on the z -axis, the axis of rotation) in the bispherical coordinate system.

Definition

The most common definition of bispherical coordinates ( σ , τ , ϕ ) is

x = a sin ⁡ σ cosh ⁡ τ − cos ⁡ σ cos ⁡ ϕ y = a sin ⁡ σ cosh ⁡ τ − cos ⁡ σ sin ⁡ ϕ z = a sinh ⁡ τ cosh ⁡ τ − cos ⁡ σ

where the σ coordinate of a point P equals the angle F 1 P F 2 and the τ coordinate equals the natural logarithm of the ratio of the distances d 1 and d 2 to the foci

τ = ln ⁡ d 1 d 2

Coordinate surfaces

Surfaces of constant σ correspond to intersecting tori of different radii

z 2 + ( x 2 + y 2 − a cot ⁡ σ ) 2 = a 2 sin 2 ⁡ σ

that all pass through the foci but are not concentric. The surfaces of constant τ are non-intersecting spheres of different radii

( x 2 + y 2 ) + ( z − a coth ⁡ τ ) 2 = a 2 sinh 2 ⁡ τ

that surround the foci. The centers of the constant- τ spheres lie along the z -axis, whereas the constant- σ tori are centered in the x y plane.

Inverse formulae

The formulae for the inverse transformation are:

σ = arccos ⁡ ( ( R 2 − a 2 ) / Q ) τ = arsinh ⁡ ( 2 a z / Q ) ϕ = atan ⁡ ( y / x )

where R = x 2 + y 2 + z 2 and Q = ( R 2 + a 2 ) 2 − ( 2 a z ) 2 .

Scale factors

The scale factors for the bispherical coordinates σ and τ are equal

h σ = h τ = a cosh ⁡ τ − cos ⁡ σ

whereas the azimuthal scale factor equals

h ϕ = a sin ⁡ σ cosh ⁡ τ − cos ⁡ σ

Thus, the infinitesimal volume element equals

d V = a 3 sin ⁡ σ ( cosh ⁡ τ − cos ⁡ σ ) 3 d σ d τ d ϕ

and the Laplacian is given by

∇ 2 Φ = ( cosh ⁡ τ − cos ⁡ σ ) 3 a 2 sin ⁡ σ [ ∂ ∂ σ ( sin ⁡ σ cosh ⁡ τ − cos ⁡ σ ∂ Φ ∂ σ ) + sin ⁡ σ ∂ ∂ τ ( 1 cosh ⁡ τ − cos ⁡ σ ∂ Φ ∂ τ ) + 1 sin ⁡ σ ( cosh ⁡ τ − cos ⁡ σ ) ∂ 2 Φ ∂ ϕ 2 ]

Other differential operators such as ∇ ⋅ F and ∇ × F can be expressed in the coordinates ( σ , τ ) by substituting the scale factors into the general formulae found in orthogonal coordinates.

Applications

The classic applications of bispherical coordinates are in solving partial differential equations, e.g., Laplace's equation, for which bispherical coordinates allow a separation of variables. However, the Helmholtz equation is not separable in bispherical coordinates. A typical example would be the electric field surrounding two conducting spheres of different radii.

References

Bispherical coordinates Wikipedia

(Text) CC BY-SA