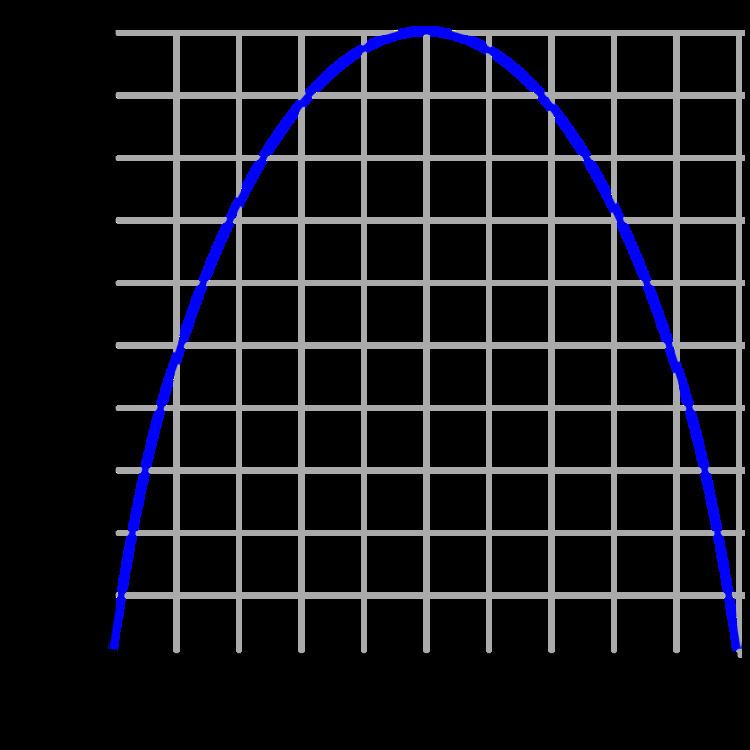
In information theory, the binary entropy function, denoted H ( p ) or H b ( p ) , is defined as the entropy of a Bernoulli process with probability of success p . Mathematically, the Bernoulli trial is modelled as a random variable X that can take on only two values: 0 and 1. The event X = 1 is considered a success and the event X = 0 is considered a failure. (These two events are mutually exclusive and exhaustive.)
If Pr ( X = 1 ) = p , then Pr ( X = 0 ) = 1 − p and the entropy of X (in shannons) is given by
H ( X ) = H b ( p ) = − p log 2 p − ( 1 − p ) log 2 ( 1 − p ) ,
where 0 log 2 0 is taken to be 0. The logarithms in this formula are usually taken (as shown in the graph) to the base 2. See binary logarithm.
When p = 1 2 , the binary entropy function attains its maximum value. This is the case of the unbiased bit, the most common unit of information entropy.
H ( p ) is distinguished from the entropy function H ( X ) in that the former takes a single real number as a parameter whereas the latter takes a distribution or random variables as a parameter. Sometimes the binary entropy function is also written as H 2 ( p ) . However, it is different from and should not be confused with the Rényi entropy, which is denoted as H 2 ( X ) .
In terms of information theory, entropy is considered to be a measure of the uncertainty in a message. To put it intuitively, suppose p = 0 . At this probability, the event is certain never to occur, and so there is no uncertainty at all, leading to an entropy of 0. If p = 1 , the result is again certain, so the entropy is 0 here as well. When p = 1 / 2 , the uncertainty is at a maximum; if one were to place a fair bet on the outcome in this case, there is no advantage to be gained with prior knowledge of the probabilities. In this case, the entropy is maximum at a value of 1 bit. Intermediate values fall between these cases; for instance, if p = 1 / 4 , there is still a measure of uncertainty on the outcome, but one can still predict the outcome correctly more often than not, so the uncertainty measure, or entropy, is less than 1 full bit.
The derivative of the binary entropy function may be expressed as the negative of the logit function:
d d p H b ( p ) = − logit 2 ( p ) = − log 2 ( p 1 − p ) .
The Taylor series of the binary entropy function in a neighborhood of 1/2 is
H b ( p ) = 1 − 1 2 ln 2 ∑ n = 1 ∞ ( 1 − 2 p ) 2 n n ( 2 n − 1 ) for 0 ≤ p ≤ 1 .