Rahul Sharma (Editor)

Arcsine distribution

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Parameters
  
none

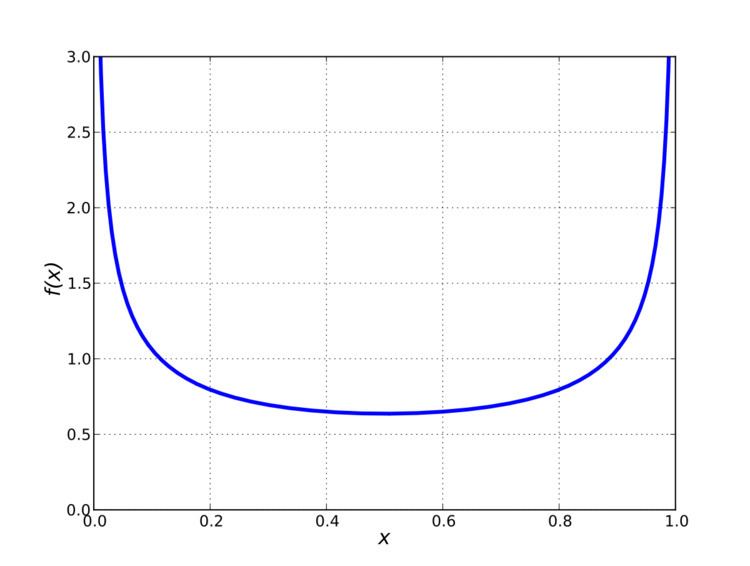Arcsine distribution

Support
  
x ∈ [ 0 , 1 ] {\displaystyle x\in [0,1]}

PDF
  
f ( x ) = 1 π x ( 1 − x ) {\displaystyle f(x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}}

CDF
  
F ( x ) = 2 π arcsin ⁡ ( x ) {\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)}

Mean
  
1 2 {\displaystyle {\frac {1}{2}}}

Median
  
1 2 {\displaystyle {\frac {1}{2}}}

In probability theory, the arcsine distribution is the probability distribution whose cumulative distribution function is

Contents

F ( x ) = 2 π arcsin ⁡ ( x ) = arcsin ⁡ ( 2 x − 1 ) π + 1 2

for 0 ≤ x ≤ 1, and whose probability density function is

f ( x ) = 1 π x ( 1 − x )

on (0, 1). The standard arcsine distribution is a special case of the beta distribution with α = β = 1/2. That is, if X is the standard arcsine distribution then X ∼ B e t a ( 1 2 , 1 2 ) .

The arcsine distribution appears

  • in the Lévy arcsine law;
  • in the Erdős arcsine law;
  • as the Jeffreys prior for the probability of success of a Bernoulli trial.

    • Arbitrary bounded support

    The distribution can be expanded to include any bounded support from a ≤ x ≤ b by a simple transformation

    F ( x ) = 2 π arcsin ⁡ ( x − a b − a )

    for a ≤ x ≤ b, and whose probability density function is

    f ( x ) = 1 π ( x − a ) ( b − x )

    on (a, b).

    Shape factor

    The generalized standard arcsine distribution on (0,1) with probability density function

    f ( x ; α ) = sin ⁡ π α π x − α ( 1 − x ) α − 1

    is also a special case of the beta distribution with parameters B e t a ( 1 − α , α ) .

    Note that when α = 1 2 the general arcsine distribution reduces to the standard distribution listed above.

    Properties

  • Arcsine distribution is closed under translation and scaling by a positive factor
  • If X ∼ A r c s i n e ( a , b )   then  k X + c ∼ A r c s i n e ( a k + c , b k + c )
  • The square of an arc sine distribution over (-1, 1) has arc sine distribution over (0, 1)
  • If X ∼ A r c s i n e ( − 1 , 1 )   then  X 2 ∼ A r c s i n e ( 0 , 1 )

    • Differential equation

    { 2 ( x − 1 ) x f ′ ( x ) + ( 2 x − 1 ) f ( x ) = 0 }

  • If U and V are i.i.d uniform (−π,π) random variables, then sin ⁡ ( U ) , sin ⁡ ( 2 U ) , − cos ⁡ ( 2 U ) , sin ⁡ ( U + V ) and sin ⁡ ( U − V ) all have an A r c s i n e ( − 1 , 1 ) distribution.
  • If X is the generalized arcsine distribution with shape parameter α supported on the finite interval [a,b] then X − a b − a ∼ B e t a ( 1 − α , α )  

    • References

    Arcsine distribution Wikipedia
    (Text) CC BY-SA