 | ||
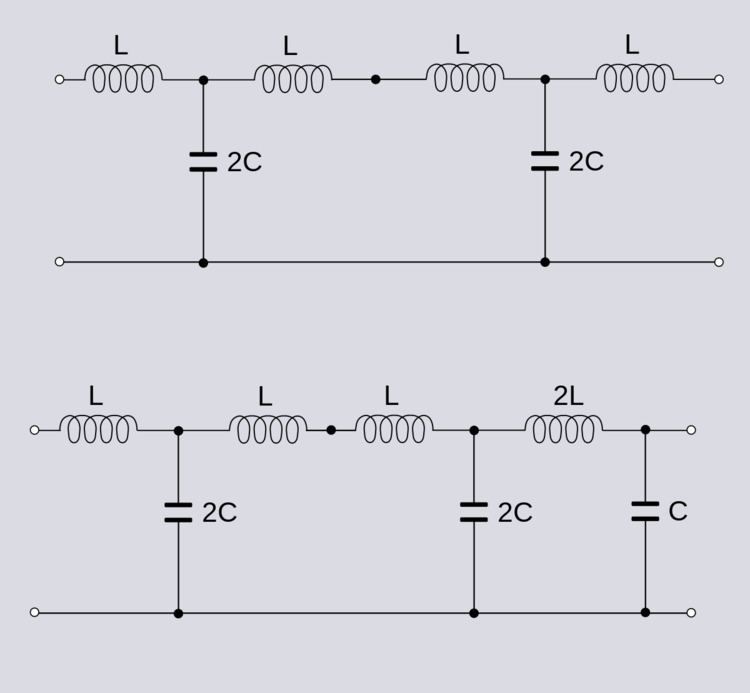
An antimetric electrical network is an electrical network that exhibits anti-symmetrical electrical properties. The term is often encountered in filter theory, but it applies to general electrical network analysis. Antimetric is the diametrical opposite of symmetric; it does not merely mean "asymmetric" (i.e., "lacking symmetry"). It is possible for networks to be symmetric or antimetric in their electrical properties without being physically or topologically symmetric or antimetric.
Contents
Definition
References to symmetry and antimetry of a network usually refer to the input impedances of a two-port network when correctly terminated. A symmetric network will have two equal input impedances, Zi1 and Zi2. For an antimetric network, the two impedances must be the dual of each other with respect to some nominal impedance R0. That is,
or equivalently
It is necessary for antimetry that the terminating impedances are also the dual of each other, but in many practical cases the two terminating impedances are resistors and are both equal to the nominal impedance R0. Hence, they are both symmetric and antimetric at the same time.
Physical and electrical antimetry
Symmetric and antimetric networks are often also topologically symmetric and antimetric, respectively. The physical arrangement of their components and values are symmetric or antimetric as in the ladder example above. However, it is not a necessary condition for electrical antimetry. For example, if the example networks of figure 1 have an additional identical T-section added to the left-hand side as shown in figure 2, then the networks remain topologically symmetric and antimetric. However, the network resulting from the application of Bartlett's bisection theorem applied to the first T-section in each network, as shown in figure 3, are neither physically symmetric nor antimetric but retain their electrical symmetric (in the first case) and antimetric (in the second case) properties.
Two-port parameters
The conditions for symmetry and antimetry can be stated in terms of two-port parameters. For a two-port network described by impedance parameters (z-parameters),
if the network is symmetric, and
if the network is antimetric. Passive networks of the kind illustrated in this article are also reciprocal, which requires that
and results in a z-parameter matrix of,
for symmetric networks and
for antimetric networks.
For a two-port network described by scattering parameters (S-parameters),
if the network is symmetric, and
if the network is antimetric. The condition for reciprocity is,
resulting in an S-parameter matrix of,
for symmetric networks and
for antimetric networks.
Applications
Some circuit designs naturally output antimetric networks. For instance, a low-pass Butterworth filter implemented as a ladder network with an even number of elements will be antimetric. Similarly, a bandpass Butterworth with an even number of resonators will be antimetric, as will a Butterworth mechanical filter with an even number of mechanical resonators.
