 | ||
In physics, angular frequency ω (also referred to by the terms angular speed, radial frequency, circular frequency, orbital frequency, radian frequency, and pulsatance) is a scalar measure of rotation rate. It refers to the angular displacement per unit time (e.g., in rotation) or the rate of change of the phase of a sinusoidal waveform (e.g., in oscillations and waves), or as the rate of change of the argument of the sine function.
Contents
Angular frequency (or angular speed) is the magnitude of the vector quantity angular velocity. The term angular frequency vector
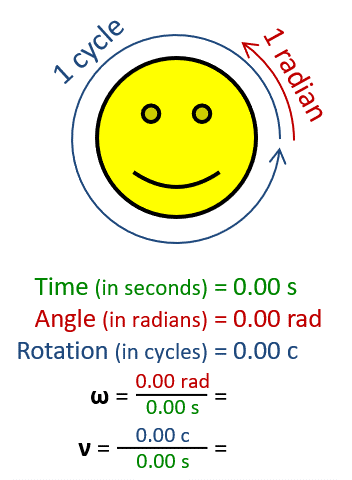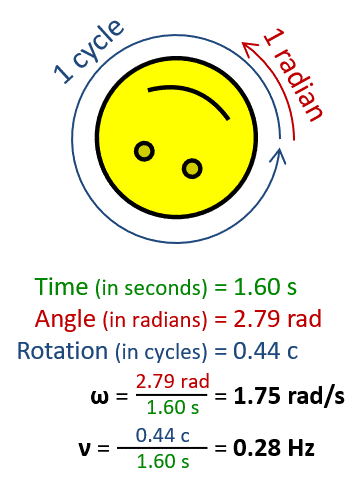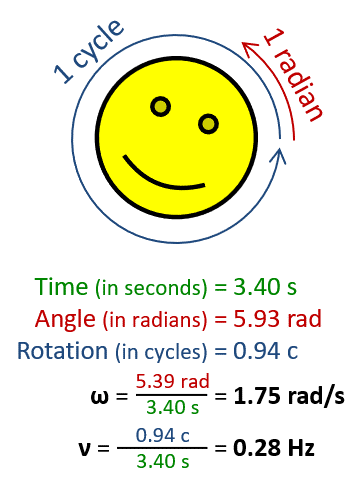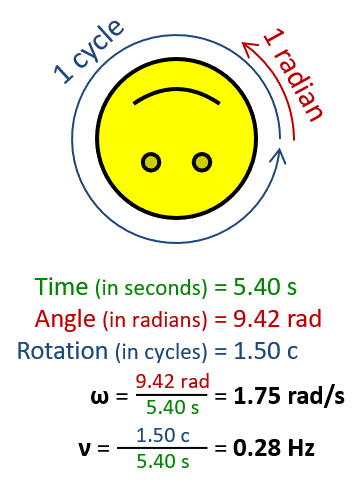
One revolution is equal to 2π radians, hence
where:
ω is the angular frequency or angular speed (measured in radians per second),T is the period (measured in seconds),f is the ordinary frequency (measured in hertz) (sometimes symbolised with ν).Units
In SI units, angular frequency is normally presented in radians per second, even when it does not express a rotational value. From the perspective of dimensional analysis, the unit hertz (Hz) is also correct, but in practice it is only used for ordinary frequency f, and almost never for ω. This convention helps avoid confusion.
In digital signal processing, the angular frequency may be normalized by the sampling rate, yielding the normalized frequency.
Circular motion
In a rotating or orbiting object, there is a relation between distance from the axis, tangential speed, and the angular frequency of the rotation:
Oscillations of a spring
An object attached to a spring will oscillate. Assuming that the spring is ideal and massless with no damping then the motion will be simple and harmonic with an angular frequency given by:
where
k is the spring constantm is the mass of the object.ω is referred to as the natural frequency (which can sometimes be denoted as ω0).
As the object oscillates, its acceleration can be calculated by
where x is displacement from an equilibrium position.
Using 'ordinary' revolutions-per-second frequency, this equation would be
LC circuits
The resonant angular frequency in a series LC circuit equals the square root of the inverse of the product of the capacitance (C measured in farads) and the inductance of the circuit (L in henrys).
Adding series resistance, for example due to the resistance of the wire in a coil, does not change the resonate frequency of the series LC circuit. For a parallel tuned circuit, the above equation is often a useful approximation, but the resonate frequency does depend on the losses of parallel elements.
