 | ||
In 3-dimensional hyperbolic geometry, the alternated hexagonal tiling honeycomb, h{6,3,3}, or , with tetrahedron and triangular tiling cells, in an octahedron vertex figure. It is named by its construction as an alteration of a hexagonal tiling honeycomb.
Contents
- Symmetry constructions
- Related honeycombs
- Cantic hexagonal tiling honeycomb
- Runcic hexagonal tiling honeycomb
- Runcicantic hexagonal tiling honeycomb
- References
A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.
Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.
Symmetry constructions
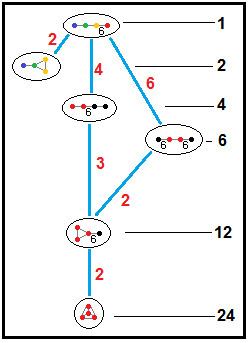
It has five alternated constructions from reflectional Coxeter groups all with four mirrors and only the first being regular: [6,3,3], [3,6,3], [6,3,6], [6,3[3]] and [3[3,3]] , having 1, 4, 6, 12 and 24 times larger fundamental domains respectively. In Coxeter notation subgroup markups, they are related as: [6,(3,3)*] (remove 3 mirrors, index 24 subgroup); [3,6,3*] or [3*,6,3] (remove 2 mirrors, index 6 subgroup); [1+,6,3,6,1+] (remove two orthogonal mirrors, index 4 subgroup); all of these are isomorphic to [3[3,3]]. The ringed Coxeter diagrams are , , , and , representing different types (colors) of hexagonal tilings in the Wythoff construction.
Related honeycombs
It has 3 related form cantic hexagonal tiling honeycomb, , runcic hexagonal tiling honeycomb, , runcicantic hexagonal tiling honeycomb, .
Cantic hexagonal tiling honeycomb
The cantic hexagonal tiling honeycomb, h2{6,3,3}, or .
Runcic hexagonal tiling honeycomb
The runcic hexagonal tiling honeycomb, h3{6,3,3}, or .
Runcicantic hexagonal tiling honeycomb
The runcicantic hexagonal tiling honeycomb, h2,3{6,3,3}, or .
