 | ||
In optics, an anti-resonant reflecting optical waveguide (ARROW) is a waveguide that uses the principle of thin-film interference to guide light with low loss. It is formed from an anti-resonant Fabry–Pérot reflector. The optical mode is leaky, but relatively low-loss propagation can be achieved by making the Fabry–Pérot reflector of sufficiently high quality or small size.
Contents
Principles of Operation
ARROW relies on the principle of thin-film interference. It is created by forming a Fabry-Perot cavity in the transverse direction, with cladding layers that function as Fabry-Perot etalons. A Fabry-Perot etalon is in resonance when the light in the layer constructively interferes with itself, resulting in high transmission. Anti-resonance occurs when the light in the layer destructively interferes with itself, resulting in no transmission through the etalon.
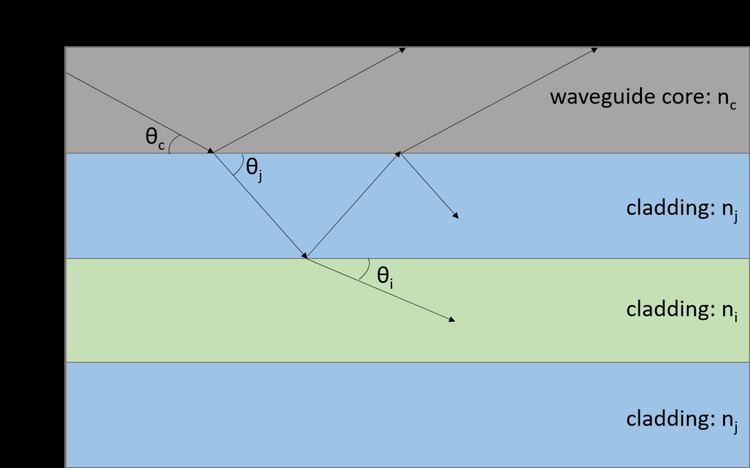
The refractive indexes of the guiding core (nc) and the cladding layers (nj, ni) are important and are carefully chosen. In order to make anti-resonance happen, nc needs to smaller than nj. In a typical system of a solid core ARROW, as shown in the figure, the waveguide consists of a low refractive index guiding core bounded on the upper surface by air and on the lower surface by higher refractive index antiresonant reflecting cladding layers. The confinement of light on the upper surface of the guiding core is provided by the total internal reflection with air, while the confinement on the lower surface is provided by interference created by the antiresonant cladding layers.
The thickness of the antiresonant cladding layer (tj) of an ARROW also needs to be carefully chosen in order to achieve anti-resonance. It can be calculated by the following formula:
while
Considerations
ARROWs can be realized as cylindrical waveguides (2D confinement) or slab waveguides (1D confinement). The latter ARROWs are practically formed by a low index layer, embedded between higher index layers. Note that the refractive indices of these ARROWs are reversed, when comparing to usual waveguides. Light is confined by total internal reflection (TIR) on the inside of the higher index layers, but achieves a lot of modal overlap with the lower index central volume.
This strong overlap can be made plausible in a simplified picture imagining "rays", as in geometrical optics. Such rays are refracted into a very shallow angle, when entering the low index inner layer. Thus, one can use the metaphor that these rays "stay very long inside" the low index inner layer. Note this is just a metaphor and the explanatory power of ray optics is very limited for the micrometer scales, at which these ARROWs are typically made.
Applications
ARROW are often used for guiding light in liquids, particularly in photonic lab-on-a-chip analytical systems (PhLoCs). Conventional waveguides rely on the principle of total internal reflection, which can only occur if the refractive index of the guiding core material is greater than the refractive indexes of its surroundings. However, the materials used to make the guiding core are typically polymer and silicon-based materials, which have higher refractive indexes (n=1.4-3.5) than that of water (n = 1.33) . As a result, a conventional hollow-core waveguide no longer works once it's filled with water solution, making the PhLoCs useless. An ARROW, on the other hand, can be liquid-filled since it confines light completely by interference, which requires that the refractive index of the guiding core to be lower than the refractive index of the surrounding materials. Thus, ARROWs become the ideal building blocks for PhLoCs.
Though ARROWs carry big advantage over conventional waveguide for building PhLoCs, they are not perfect. The main problem of ARROW is its undesirable light loss. Light loss of ARROWs decreases the signal to noise ratio of the PhLoCs. Different versions of ARROWs have been designed and tested in order to overcome this problem.
