 | ||
In music, 53 equal temperament, called 53-TET, 53-EDO, or 53-ET, is the tempered scale derived by dividing the octave into 53 equal steps (equal frequency ratios). Play Each step represents a frequency ratio of 21/53, or 22.6415 cents ( Play ), an interval sometimes called the Holdrian comma.
Contents
- History
- Comparison to other scales
- Theoretical properties
- Notation
- Chords of 53 equal temperament
- Music
- References
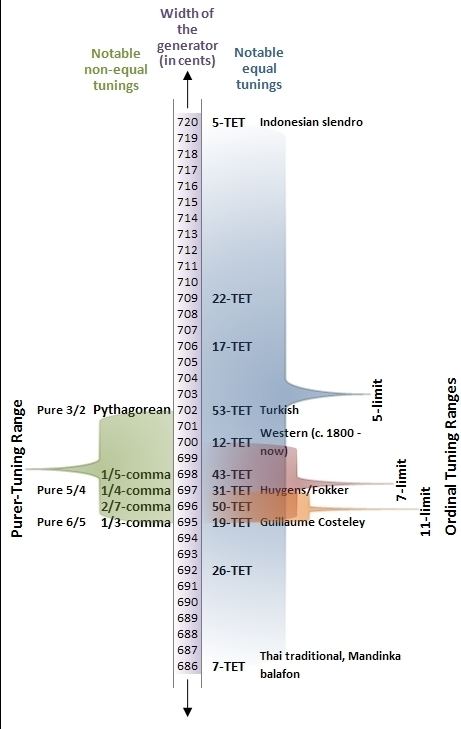
53-TET is a tuning of equal temperament in which the tempered perfect fifth is 701.89 cents wide, as shown in Figure 1.
History
Theoretical interest in this division goes back to antiquity. Ching Fang (78–37 BC), a Chinese music theorist, observed that a series of 53 just fifths (
After Mercator, William Holder published a treatise in 1694 which pointed out that 53 equal temperament also very closely approximates the just major third (to within 1.4 cents), and consequently 53 equal temperament accommodates the intervals of 5-limit just intonation very well. This property of 53-TET may have been known earlier; Isaac Newton's unpublished manuscripts suggest that he had been aware of it as early as 1664–65.
Comparison to other scales
Because a distance of 31 steps in this scale is almost precisely equal to a just perfect fifth, in theory this scale can be considered a form of Pythagorean tuning that has been extended to 53 tones. As such the intervals available can have the same properties as any Pythagorean tuning, such as fifths that are (practically) pure, major thirds that are wide from just (about 81/64 opposed to the purer 5/4), and minor thirds that are conversely narrow (32/27 compared to 6/5).
However, 53-TET contains additional intervals that are very close to just intonation. For instance, the interval of 17 steps is also a major third, but only 1.4 cents narrower than the very pure just interval 5/4. 53-TET is very good as an approximation to any interval in 5-limit just intonation.
The matches to the just intervals involving the 7th harmonic are slightly less close, but all such intervals are still matched with the highest deviation being the 7:5 tritone. The 11th harmonic and intervals involving it are less closely matched, as illustrated with the undecimal neutral seconds and thirds in the table below.
Theoretical properties
The 53-ET tuning equates to the unison, or tempers out, the intervals 32805/32768, known as the schisma, and 15625/15552, known as the kleisma. These are both 5-limit intervals, involving only the primes 2, 3 and 5 in their factorization, and the fact that 53-ET tempers out both characterizes it completely as a 5-limit temperament: it is the only regular temperament tempering out both of these intervals, or commas, a fact which seems to have first been recognized by Japanese music theorist Shohé Tanaka. Because it tempers these out, 53-ET can be used for both schismatic temperament, tempering out the schisma, and Hanson temperament (also called kleismic), tempering out the kleisma.
The interval of 7/4 is 4.8 cents sharp in 53-ET, and using it for 7-limit harmony means that the septimal kleisma, the interval 225/224, is also tempered out.
Notation
Attempting to use standard notation, seven letter notes plus sharps or flats, can quickly become confusing. This is unlike the case with 19-ET and 31-ET where there is little ambiguity. By not being meantone, it adds some problems that require more attention. Specifically, the major third is different from a ditone, two tones, each of which is two fifths minus an octave. Likewise, the minor third is different from a semiditone. The fact that the syntonic comma is not tempered out means that notes and intervals need to be defined more precisely.
Chords of 53 equal temperament
Standard musical notation can be used to denote 53 equal temperament; however, since it is a Pythagorean system, with nearly pure fifths, major and minor triads cannot be spelled in the same manner as in a meantone tuning. Instead, the major triads are chords like C-F♭-G, where the major third is a diminished fourth; this is the defining characteristic of schismatic temperament. Likewise, the minor triads are chords like C-D♯-G. In 53-ET the dominant seventh chord would be spelled C-F♭-G-B♭, but the otonal tetrad is C-F♭-G-C, and C-F♭-G-A♯ is still another seventh chord. The utonal tetrad, the inversion of the otonal tetrad, is spelled C-D♯-G-G.
Further septimal chords are the diminished triad, having the two forms C-D♯-G♭ and C-F-G♭, the subminor triad, C-F-G, the supermajor triad C-D-G, and corresponding tetrads C-F-G-B and C-D-G-A♯. Since 53-ET tempers out the septimal kleisma, the septimal kleisma augmented triad C-F♭-B in its various inversions is also a chord of the system. So is the orwell tetrad, C-F♭-D-G in its various inversions.
Because 53-TET is compatible with both the schismatic temperament and the syntonic temperament, it can be used as a pivot tuning in a temperament modulation (a musical effect enabled by dynamic tonality).
Music
In the 19th century, people began devising instruments in 53-et, with an eye to their use in playing near-just 5-limit music. Such instruments were devised by RHM Bosanquet and the American tuner James Paul White. Subsequently the temperament has seen occasional use by composers in the west, and has been used in Turkish music as well; the Turkish composer Erol Sayan has employed it, following theoretical use of it by Turkish music theorist Kemal Ilerici. Arabic music, which for the most part bases its theory on quartertones, has also made some use of it; the Syrian violinist and music theorist Twfiq Al-Sabagh proposed that instead of an equal division of the octave into 24 parts a 24-note scale in 53-et should be used as the master scale for Arabic music.
Croatian composer Josip Štolcer-Slavenski wrote one piece, which has never been published, which uses Bosanquet's Enharmonium during its first movement, entitled Music for Natur-ton-system. Furthermore, General Thompson worked in league with the London-based guitar maker Louis Panormo to produce the Enharmonic Guitar (see: James Westbrook,‘General Thompson’s Enharmonic Guitar’, Soundboard: XXXVIII: 4, pp. 45–52.).
