Equal temperament

History

The two figures frequently credited with the achievement of exact calculation of equal temperament are Zhu Zaiyu (also romanized as Chu-Tsaiyu. Chinese: 朱載堉) in 1584 and Simon Stevin in 1585. According to Fritz A. Kuttner, a critic of the theory, it is known that "Chu-Tsaiyu presented a highly precise, simple and ingenious method for arithmetic calculation of equal temperament mono-chords in 1584" and that "Simon Stevin offered a mathematical definition of equal temperament plus a somewhat less precise computation of the corresponding numerical values in 1585 or later." The developments occurred independently.

Kenneth Robinson attributes the invention of equal temperament to Zhu Zaiyu and provides textual quotations as evidence. Zhu Zaiyu is quoted as saying that, in a text dating from 1584, "I have founded a new system. I establish one foot as the number from which the others are to be extracted, and using proportions I extract them. Altogether one has to find the exact figures for the pitch-pipers in twelve operations." Kuttner disagrees and remarks that his claim "cannot be considered correct without major qualifications." Kuttner proposes that neither Zhu Zaiyu or Simon Stevin achieved equal temperament, and that neither of the two should be treated as inventors.

Early history

The origin of the Chinese pentatonic scale is traditionally ascribed to the mythical Ling Lun. Allegedly his writings discussed the equal division of the scale in the 27th century BC. However, evidence of the origins of writing in this period (the early Longshan) in China is limited to rudimentary inscriptions on oracle bones and pottery.

A complete set of bronze chime bells, among many musical instruments found in the tomb of the Marquis Yi of Zeng (early Warring States, c. 5th century BCE in the Chinese Bronze Age), covers 5 full 7 note octaves in the key of C Major, including 12 note semi-tones in the middle of the range.

An approximation for equal temperament was described by He Chengtian, a mathematician of Southern and Northern Dynasties around 400 AD. He came out with the earliest recorded approximate numerical sequence in relation to equal temperament in history: 900 849 802 758 715 677 638 601 570 536 509.5 479 450.

Historically, there was a seven-equal temperament or hepta-equal temperament practice in Chinese tradition.

Zhu Zaiyu (朱載堉), a prince of the Ming court, spent thirty years on research based on the equal temperament idea originally postulated by his father. He described his new pitch theory in his Fusion of Music and Calendar 乐律融通 published in 1580. This was followed by the publication of a detailed account of the new theory of the equal temperament with a precise numerical specification for 12-TET in his 5,000-page work Complete Compendium of Music and Pitch (Yuelü quan shu 乐律全书) in 1584. An extended account is also given by Joseph Needham. Zhu obtained his result mathematically by dividing the length of string and pipe successively by ¹²√2 ≈ 1.059463, and for pipe length by ²⁴√2, such that after twelve divisions (an octave) the length was divided by a factor of 2:

(¹²√2)¹² = 2.

Similarly, after 84 divisions (7 octaves) the length was divided by a factor of 128:

(¹²√2)⁸⁴ = 2⁷ = 128.

Zhu Zaiyu

According to Gene Cho, Zhu Zaiyu was the first person to solve the equal temperament problem mathematically. Matteo Ricci, a Jesuit in China recorded this work in his personal journal and very likely brought it back to the West. In 1620, Zhu's work was referenced by a European mathematician. Murray Barbour said, "The first known appearance in print of the correct figures for equal temperament was in China, where Prince Tsaiyü's brilliant solution remains an enigma." The 19th-century German physicist Hermann von Helmholtz wrote in On the Sensations of Tone that a Chinese prince (see below) introduced a scale of seven notes, and that the division of the octave into twelve semitones was discovered in China.

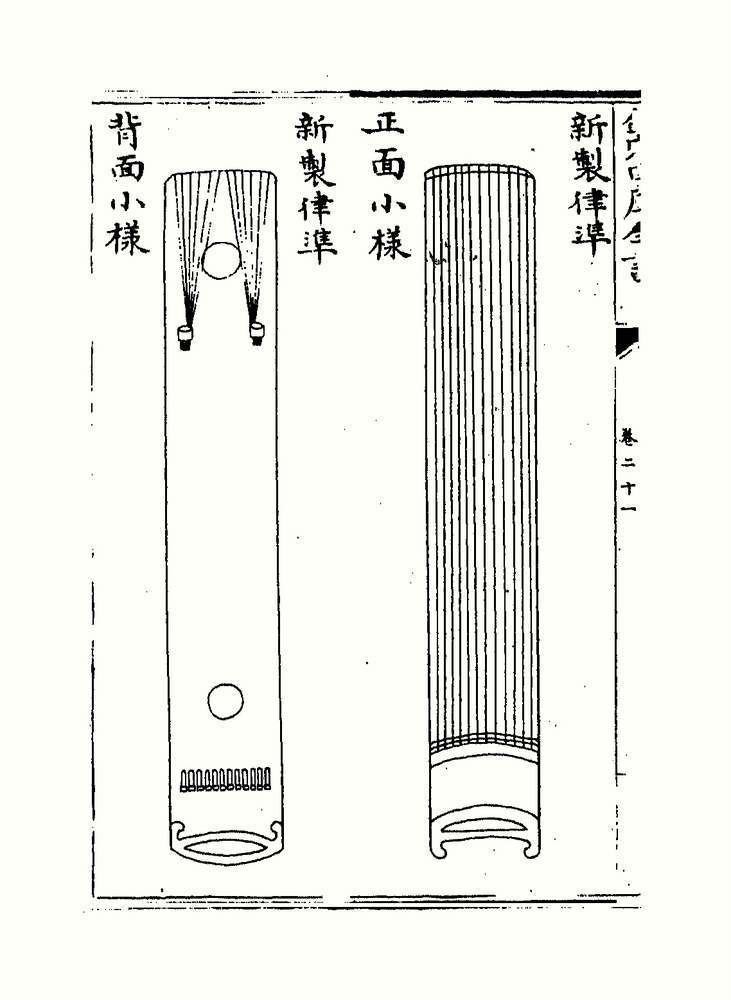
Zhu Zaiyu illustrated his equal temperament theory by construction of a set of 36 bamboo tuning pipes ranging in 3 octaves, with instructions of the type of bamboo, color of paint, and detailed specification on their length and inner and outer diameters. He also constructed a 12-string tuning instrument, with a set of tuning pitch pipes hidden inside its bottom cavity. In 1890, Victor-Charles Mahillon, curator of the Conservatoire museum in Brussels, duplicated a set of pitch pipes according to Zhu Zaiyu's specification. He said that the Chinese theory of tones knew more about the length of pitch pipes than its Western counterpart, and that the set of pipes duplicated according to the Zaiyu data proved the accuracy of this theory.

Early history

One of the earliest discussions of equal temperament occurs in the writing of Aristoxenus in the 4th century BC.

Vincenzo Galilei (father of Galileo Galilei) was one of the first practical advocates of twelve-tone equal temperament. He composed a set of dance suites on each of the 12 notes of the chromatic scale in all the "transposition keys", and published also, in his 1584 "Fronimo", 24 + 1 ricercars. He used the 18:17 ratio for fretting the lute (although some adjustment was necessary for pure octaves).

Galilei's countryman and fellow lutenist Giacomo Gorzanis had written music based on equal temperament by 1567. Gorzanis was not the only lutenist to explore all modes or keys: Francesco Spinacino wrote a "Recercare de tutti li Toni" (Ricercar in all the Tones) as early as 1507. In the 17th century lutenist-composer John Wilson wrote a set of 30 preludes including 24 in all the major/minor keys.

Henricus Grammateus drew a close approximation to equal temperament in 1518. The first tuning rules in equal temperament were given by Giovani Maria Lanfranco in his "Scintille de musica". Zarlino in his polemic with Galilei initially opposed equal temperament but eventually conceded to it in relation to the lute in his Sopplimenti musicali in 1588.

Simon Stevin

The first mention of equal temperament related to the twelfth root of two in the West appeared in Simon Stevin's manuscript Van De Spiegheling der singconst (ca. 1605), published posthumously nearly three centuries later in 1884. However, due to insufficient accuracy of his calculation, many of the chord length numbers he obtained were off by one or two units from the correct values. As a result, the frequency ratios of Simon Stevin's chords has no unified ratio, but one ratio per tone, which is claimed by Gene Cho as incorrect.

The following were Simon Stevin's chord length from Van de Spiegheling der singconst:

A generation later, French mathematician Marin Mersenne presented several equal tempered chord lengths obtained by Jean Beaugrand, Ismael Bouillaud, and Jean Galle.

In 1630 Johann Faulhaber published a 100 cent monochord table, which contained several errors due to his use of logarithmic tables. He did not explain how he obtained his results.

Baroque era

From 1450 to about 1800, plucked instrument players (lutenists and guitarists) generally favored equal temperament, and the Brossard lute Manuscript compiled in the last quarter of the 17th century contains a series of 18 preludes attributed to Bocquet written in all keys, including the last prelude, entitled Prelude sur tous les tons, which enharmonically modulates through all keys. Angelo Michele Bartolotti published a series of passacaglias in all keys, with connecting enharmonically modulating passages. Among the 17th-century keyboard composers Girolamo Frescobaldi advocated equal temperament. Some theorists, such as Giuseppe Tartini, were opposed to the adoption of equal temperament; they felt that degrading the purity of each chord degraded the aesthetic appeal of music, although Andreas Werckmeister emphatically advocated equal temperament in his 1707 treatise published posthumously.

J. S. Bach wrote The Well-Tempered Clavier to demonstrate the musical possibilities of well temperament, where in some keys the consonances are even more degraded than in equal temperament. It is possible that when composers and theoreticians of earlier times wrote of the moods and "colors" of the keys, they each described the subtly different dissonances made available within a particular tuning method. However, it is difficult to determine with any exactness the actual tunings used in different places at different times by any composer. (Correspondingly, there is a great deal of variety in the particular opinions of composers about the moods and colors of particular keys.)

Twelve tone equal temperament took hold for a variety of reasons. It was a convenient fit for the existing keyboard design, and permitted total harmonic freedom at the expense of just a little impurity in every interval. This allowed greater expression through enharmonic modulation, which became extremely important in the 18th century in music of such composers as Francesco Geminiani, Wilhelm Friedemann Bach, Carl Philipp Emmanuel Bach and Johann Gottfried Müthel.

The progress of equal temperament from the mid-18th century on is described with detail in quite a few modern scholarly publications: it was already the temperament of choice during the Classical era (second half of the 18th century), and it became standard during the Early Romantic era (first decade of the 19th century), except for organs that switched to it more gradually, completing only in the second decade of the 19th century. (In England, some cathedral organists and choirmasters held out against it even after that date; Samuel Sebastian Wesley, for instance, opposed it all along. He died in 1876.)

A precise equal temperament is possible using the 17th-century Sabbatini method of splitting the octave first into three tempered major thirds. This was also proposed by several writers during the Classical era. Tuning without beat rates but employing several checks, achieving virtually modern accuracy, was already done in the first decades of the 19th century. Using beat rates, first proposed in 1749, became common after their diffusion by Helmholtz and Ellis in the second half of the 19th century. The ultimate precision was available with 2-decimal tables published by White in 1917.

It is in the environment of equal temperament that the new styles of symmetrical tonality and polytonality, atonal music such as that written with the twelve tone technique or serialism, and jazz (at least its piano component) developed and flourished.

General properties

In an equal temperament, the distance between two adjacent steps of the scale is the same interval. Because the perceived identity of an interval depends on its ratio, this scale in even steps is a geometric sequence of multiplications. (An arithmetic sequence of intervals would not sound evenly spaced, and would not permit transposition to different keys.) Specifically, the smallest interval in an equal-tempered scale is the ratio:

rⁿ = p r = ⁿ√p

where the ratio r divides the ratio p (typically the octave, which is 2:1) into n equal parts. (See Twelve-tone equal temperament below.)

Scales are often measured in cents, which divide the octave into 1200 equal intervals (each called a cent). This logarithmic scale makes comparison of different tuning systems easier than comparing ratios, and has considerable use in Ethnomusicology. The basic step in cents for any equal temperament can be found by taking the width of p above in cents (usually the octave, which is 1200 cents wide), called below w, and dividing it into n parts:

c = w/n

In musical analysis, material belonging to an equal temperament is often given an integer notation, meaning a single integer is used to represent each pitch. This simplifies and generalizes discussion of pitch material within the temperament in the same way that taking the logarithm of a multiplication reduces it to addition. Furthermore, by applying the modular arithmetic where the modulus is the number of divisions of the octave (usually 12), these integers can be reduced to pitch classes, which removes the distinction (or acknowledges the similarity) between pitches of the same name, e.g. c is 0 regardless of octave register. The MIDI encoding standard uses integer note designations.

Background theory

Basic concepts:

From logarithms: The logarithm of a number is the exponent to which another fixed number, the base, must be raised to produce that number. For example: (9/8)² = 81/64. The logarithm of 81/64 to base 9/8 is 2, or

log 9 8 ⁡ 81 64 = 2.

To compare logarithms, we use some standard base, e.g. 10 or e. Usually, in mathematical notation "log" means "logarithm with base 10". For example: log 9/8 = log 1.125 = 0.0511525224473813, and, log (9/8)² = log 81/64 = log 1.265625 = 0.1023050448947626. The latter logarithm divided by the former yields 2, the exponent as above.

From physics: For a given velocity of the wave on the string, length and frequency of the sound produced from a string when it is plucked, are inverse proportional (Equation 2). According to Equation 1, for the same tension in the string, and the same string’s linear density, the velocity of the wave on the string is the same.

From acoustics: Pitch is the distinctive quality of a sound, dependent primarily on the [fundamental] frequency of the sound waves produced by its source.

Psychoacoustical law: It was known to Pythagoras and perhaps to ancient Chinese philosophers, that our subjective sensation of the difference (interval) in pitch (tone) is inversely proportional to the exponent of the ratio of string (chord) lengths. In modern terms, it is proportional to the logarithm of the ratio of fundamental frequencies of sounds produced by two different lengths of the string.

Example

Consider two pairs of a string's lengths: 90 cm, 80 cm, and, 81 cm, 64 cm. Our subjective sensation of pitch difference (interval) between the sounds produced by string's lengths 81 cm and 64 cm, the ratio 81/64 = (9/8)², is double that between 90 cm and 80 cm, the ratio 90/80 = 9/8 (see above, From logarithms and Psychoacoustical law). However the pitch of sound from the 90 cm is lower than that from the 80 cm, and from the 81 cm is lower than that from the 64 cm. Now consider two pairs of fundamental frequencies (from other lengths): 90 Hz/80 Hz and 81 Hz/64 Hz. Our subjective sensation of the ratio 81/64 = (9/8)² is also twice that of 90/80 = 9/8, but the pitch of 90 Hz is higher than that of 80 Hz, and that of 81 Hz higher than that of 64 Hz. The greater the string's length, the lesser the fundamental frequency, and the lower the pitch.

Let A and B be two periodic sounds with stable fundamental frequencies (stimuli) ffreq_A and ffreq_B. Then, the ratio ffreq_A/ffreq_B is called the ratio interval. Our subjective sensation of the interval between these sounds is proportional to log ffreq_A/ffreq_B.

Let C and D be two other periodic sounds with stable fundamental frequencies: ffreq_C and ffreq_D. Their ratio interval is ffreq_C/ffreq_D. Let

m = log ⁡ f f r e q A f f r e q B log ⁡ f f r e q C f f r e q D

(see above, logarithms, second example, and below, main formula for d = 1). Then

l o g f f r e q A f f r e q B = m ⋅ log ⁡ f f r e q C f f r e q D .

Our subjective sensation of the sound interval A/B (represented by log ffreq_A/ffreq_B), is proportional, by proportion m, to our subjective sensation (represented by log ffreq_C/ffreq_D) of the sound interval C/D. The proportion m is magnitude, and log ffreq_C/ffreq_D the unit for the tempered interval A/B.

Indeed, if we multiply in the last equation m by d; m′ = td, and divide log ffreq_C/ffreq_D by d, then m' is the magnitude and

log ⁡ f f r e q C f f r e q D d

is the unit, as with every quantity, e.g. length L = 5 m. If the magnitude 5 is multiplied by 100, and m (certain length, serving as unit) divided by 100 (that is, cm), then L = 500 cm.

Let t(r) be the tempered interval of ratio interval r. Then we have:

t ( r ) = log ⁡ r = m ⋅ log ⁡ b d ,

where m is magnitude and log b/d is the unit of tempered interval. The main formula below is obtained from this one.

In the example 2 of the main formula, it is

log ⁡ 3 2 log ⁡ 9 8 = 3.442... ,

which means our subjective sensation of the ratio interval 3/2 (a perfect fifth) is 3.442 times our subjective sensation of the ratio interval 9/8 (a major second). The number 3.442 is the magnitude, and the tempered interval t(9/8) = log 9/8 is the unit of tempered interval t(3/2) = log 3/2. Multiplying by 100 yields 344.2 hundredths of the tempered interval t(9/8).

Note: Pitch depends to a lesser degree on the sound pressure level (loudness, volume) of the tone, especially at frequencies below 1,000 Hz and above 2,000 Hz. The pitch of lower tones gets lower as sound pressure increases. For instance, a tone of 200 Hz that is very loud seems one semitone lower in pitch than if it is just barely audible. Above 2,000 Hz, the pitch gets higher as the sound gets louder. See Pitch and frequency (last paragraph).

Main formula

m = log ⁡ r log ⁡ b ⋅ d

where m is the magnitude of tempered interval, r the ratio interval, b the base interval (2 for octave) and d the divisor of base interval (1200 for cents).

Here are some examples of the formula:

1. Ratio interval r = 3/2, and unit cent (b = 2 and d = 1200), then m = 701.955... and t(3/2) = 701.955 cents.
2. Ratio interval r = 3/2, and unit hundredth of the whole tone 9/8 (b = 9/8 and d = 100), then m = 344.247... and t(3/2) = 344.247 hundredths of the whole tone.
3. Ratio interval r = 2 (octave) and unit hundredth of the whole tone 9/8 (b = 9/8 and d = 100), then m = 588.4949... and t(2) = 588.4949 hundredths of the whole tone.
4. Ratio interval r = 2 (octave), and unit hundredth of Pythagorean limma (b = 256/243 and d = 100), then m = 1330 and t(2) = 1330 hundredths of Pythagorean limma.
5. Ratio interval r = 800/729 (idiosyncratic of Byzantine music), and unit tenth of Pythagorean comma (b = 531441/524288 and d = 10), then m = 68.58... and t(800/729) = 68.58 tenths of Pythagorean comma.
6. Ratio interval r = 256/243 (Pythagorean limma), and unit hundredth of the fourth (b = 4/3 and d = 100), then m = 18.1158... and t(r) = 18.1158 hundredths of the fourth.
7. Ratio interval r = 9/8 (whole tone), and unit hundredth of the fourth (b = 4/3 and d = 100), then m = 40.942... and t(9/8) = 40.942 hundredths of the fourth.
8. Ratio interval r = 1.359 (1 plus random decimal 359), and unit cent (b = 2 and d = 1200), then m = 531.05... and t(1.359) = 531.05 cents.
9. Ratio interval r = 0.052 (random decimal part), and unit cent (b = 2 and d = 1200), then m = -5118 and t(0.052) = −5118 cents.
10. Ratio interval r = 1, and unit cent (b = 2 and d = 1200), then m = 0 and t(1) = 0 cents.

Derived formula

r = b m d

where r, b, d, m are as in the main formula, above. This can be obtained by taking the exponent of each side in the main formula.

1. When b = 2 (octave), d = 1200, m = 100 (tempered semitone), then r = 1.0594630943592953, ratio interval of tempered semitone.
2. When b = 9/8 (whole tone), d = 100, m = 344.247..., then r = 1.5 = 3/2 (perfect fifth). Compare '2nd e in the main formula.
3. When b = 256/243, d = 100, m = 226, then r = 1.125 = 9/8 (whole tone).
4. When b = 256/243, d = 100, m = 1330, then r = 2 (octave). Compare example 4 under the main formula.
5. When b = 256/243, d = 100, m = 655 (random number), then r = 1.406859...
6. When t(r) = −351 (random) cents (b = 2, d = 1200), then r = 0.816485969595...
7. Let note NH = 250 Hz, and we need some note's frequency NH plus 9/8, plus 800/729, minus (hyphesis) 1/3 of t(256/243) (tempered Pythagorean limma). Calculation is following:

Notes

The numbers r, m, b, d could be random under following conditions:

1. The magnitude (m) can be any real number.
2. The ratio interval (r) must be a positive number: r > 0.
3. The base interval (b) must be greater than unity: b > 1.
4. The divisor (d) must be a natural number: d = 1, 2, 3, ...

The relations between r and m are:

When 0 < r < 1, then m < 0.

When r = 1, then m = 0.

When r > 1, then m > 0.

as with logarithms in general.

In twelve-tone equal temperament, which divides the octave into 12 equal parts, the width of a semitone, i.e. the frequency ratio of the interval between two adjacent notes, is the twelfth root of two:

¹²√2 = 2^1⁄₁₂ ≈ 1.059463

This interval is divided into 100 cents.

Calculating absolute frequencies

To find the frequency, P_n, of a note in 12-TET, the following definition may be used:

P_n = P_a(¹²√2)^{(n − a)}

In this formula P_n refers to the pitch, or frequency (usually in hertz), you are trying to find. P_a refers to the frequency of a reference pitch (usually 440Hz). n and a refer to numbers assigned to the desired pitch and the reference pitch, respectively. These two numbers are from a list of consecutive integers assigned to consecutive semitones. For example, A₄ (the reference pitch) is the 49th key from the left end of a piano (tuned to 440 Hz), and C₄ (middle C) is the 40th key. These numbers can be used to find the frequency of C₄:

P₄₀ = 440(¹²√2)^{(40 − 49)} ≈ 261.626 Hz

Comparison to just intonation

The intervals of 12-TET closely approximate some intervals in just intonation. The fifths and fourths are almost indistinguishably close to just.

In the following table the sizes of various just intervals are compared against their equal-tempered counterparts, given as a ratio as well as cents.

Seven-tone equal division of the fifth

Violins, violas and cellos are tuned in perfect fifths (G – D – A – E, for violins, and C – G – D – A, for violas and cellos), which suggests that their semi-tone ratio is slightly higher than in the conventional twelve-tone equal temperament. Because a perfect fifth is in 3:2 relation with its base tone, and this interval is covered in 7 steps, each tone is in the ratio of ⁷√ ³⁄₂ to the next (100.28 cents), which provides for a perfect fifth with ratio of 3:2 but a slightly widened octave with a ratio of ≈ 517:258 or ≈ 2.00388:1 rather than the usual 2:1 ratio, because twelve perfect fifths do not equal seven octaves. During actual play, however, the violinist chooses pitches by ear, and only the four unstopped pitches of the strings are guaranteed to exhibit this 3:2 ratio.

5 and 7 tone temperaments in ethnomusicology

Five and seven tone equal temperament (5-TET  Play  and 7-TET Play  ), with 240  Play  and 171  Play  cent steps respectively, are fairly common. A Thai xylophone measured by Morton (1974) "varied only plus or minus 5 cents," from 7-TET. A Ugandan Chopi xylophone measured by Haddon (1952) was also tuned to this system. According to Morton, "Thai instruments of fixed pitch are tuned to an equidistant system of seven pitches per octave ... As in Western traditional music, however, all pitches of the tuning system are not used in one mode (often referred to as 'scale'); in the Thai system five of the seven are used in principal pitches in any mode, thus establishing a pattern of nonequidistant intervals for the mode."  Play  Indonesian gamelans are tuned to 5-TET according to Kunst (1949), but according to Hood (1966) and McPhee (1966) their tuning varies widely, and according to Tenzer (2000) they contain stretched octaves. It is now well-accepted that of the two primary tuning systems in gamelan music, slendro and pelog, only slendro somewhat resembles five-tone equal temperament while pelog is highly unequal; however, Surjodiningrat et al. (1972) has analyzed pelog as a seven-note subset of nine-tone equal temperament (133 cent steps  Play ). A South American Indian scale from a preinstrumental culture measured by Boiles (1969) featured 175 cent seven tone equal temperament, which stretches the octave slightly as with instrumental gamelan music.

5-TET and 7-TET mark the endpoints of the syntonic temperament's valid tuning range, as shown in Figure 1.

In 5-TET the tempered perfect fifth is 720 cents wide (at the top of the tuning continuum), and marks the endpoint on the tuning continuum at which the width of the minor second shrinks to a width of 0 cents.

In 7-TET the tempered perfect fifth is 686 cents wide (at the bottom of the tuning continuum), and marks the endpoint on the tuning continuum, at which the minor second expands to be as wide as the major second (at 171 cents each).

Various Western equal temperaments

24-EDO, the quarter tone scale (or 24-TET), was a popular microtonal tuning In the 20th century probably because it represented a convenient access point for composers conditioned on standard Western 12-EDO pitch and notation practices who were also interested in microtonality. Because 24-EDO contains all of the pitches of 12-EDO plus new pitches halfway between each adjacent pair of 12-EDO pitches, they could employ the additional colors without losing any tactics available in 12-tone harmony. The fact that 24 is a multiple of 12 also made 24-EDO easy to achieve instrumentally by employing two traditional 12-EDO instruments purposely tuned a quarter-tone apart, such as two pianos, which also allowed each performer (or one performer playing a different piano with each hand) to read familiar 12-tone notation. Various composers including Charles Ives experimented with music for quarter-tone pianos.

27-EDO is the smallest EDO that uniquely represents all intervals involving the first eight harmonics. It tempers out the septimal comma but not the syntonic comma.

29-TET is the lowest number of equal divisions of the octave that produces a better perfect fifth than 12-TET. Its major third is roughly as inaccurate as 12-TET; however, it is tuned 14 cents flat rather than 14 cents sharp. It tunes the 7th, 11th, and 13th harmonics flat as well, by roughly the same amount. This means intervals such as 7:5, 11:7, 13:11, etc., are all matched extremely well in 29-TET.

31 tone equal temperament was advocated by Christiaan Huygens and Adriaan Fokker. 31-TET has a slightly less accurate fifth than 12-TET, but provides near-just major thirds, and provides decent matches for harmonics up to at least 13, of which the seventh harmonic is particularly accurate.

34 EDO gives slightly less total combined errors of approximation to the 5-limit just ratios 3:2, 5:4, 6:5, and their inversions than 31 EDO does, although the approximation of 5:4 is worse. 34 EDO doesn't approximate ratios involving prime 7 well. It contains a 600-cent tritone, since it is an even-numbered EDO.

41-TET is the second lowest number of equal divisions that produces a better perfect fifth than 12-TET. Its major third is more accurate than 12-ET and 29-ET, about 6 cents flat.

53-TET is better at approximating the traditional just consonances than 12, 19 or 31-TET, but has had only occasional use. Its extremely good perfect fifths make it interchangeable with an extended Pythagorean tuning, but it also accommodates schismatic temperament, and is sometimes used in Turkish music theory. It does not, however, fit the requirements of meantone temperaments, which put good thirds within easy reach via the cycle of fifths. In 53-TET the very consonant thirds would be reached instead by strange enharmonic relationships like C–F♭, as it is an example of schismatic temperament. A consequence of this is that chord progressions like I–vi–ii–V–I won't land you back where you started in 53-TET, but rather one 53-tone step flat (unless the motion by I–vi wasn't by the 5-limit minor third).

72-TET approximates many just intonation intervals well, even into the 7-limit and 11-limit, such as 7:4, 9:7, 11:5, 11:6 and 11:7. 72-TET has been taught, written and performed in practice by Joe Maneri and his students (whose atonal inclinations interestingly typically avoid any reference to just intonation whatsoever). It can be considered an extension of 12 EDO because 72 is a multiple of 12. 72 EDO has a smallest interval that is six times smaller than the smallest interval of 12 EDO and therefore contains six copies of 12 EDO starting on different pitches. It also contains three copies of 24 EDO and two copies of 36 EDO, which are themselves multiples of 12 EDO.

Other equal divisions of the octave that have found occasional use include, 15-TET, 17-TET, 19-TET and 22-TET.

2, 5, 12, 41, 53, 306, 665 and 15601 are denominators of first convergents of log₂(3), so 2, 5, 12, 41, 53, 306, 665 and 15601 twelfths (and fifths), being in correspondent equal temperaments equal to an integer number of octaves, are better approximation of 2, 5, 12, 41, 53, 306, 665 and 15601 just twelfths/fifths than for any equal temperaments with less tones.

1, 2, 3, 5, 7, 12, 29, 41, 53, 200... (sequence A060528 in the OEIS) is the sequence of divisions of octave that provide better and better approximations of the perfect fifth. Related sequences contain divisions approximating other just intervals. It is noteworthy that many elements of this sequences are sums of previous elements.

This application: [2] calculates the frequencies, approximate cents, and MIDI pitch bend values for any systems of equal division of the octave. Note that 'rounded' and 'floored' produce the same MIDI pitch bend value.

Equal temperaments of non-octave intervals

The equal-tempered version of the Bohlen–Pierce scale consists of the ratio 3:1, 1902 cents, conventionally a perfect fifth plus an octave (that is, a perfect twelfth), called in this theory a tritave ( play ), and split into a thirteen equal parts. This provides a very close match to justly tuned ratios consisting only of odd numbers. Each step is 146.3 cents ( play ), or ¹³√3.

Wendy Carlos created three unusual equal temperaments after a thorough study of the properties of possible temperaments having a step size between 30 and 120 cents. These were called alpha, beta, and gamma. They can be considered as equal divisions of the perfect fifth. Each of them provides a very good approximation of several just intervals. Their step sizes:

alpha: ⁹√ ³⁄₂ (78.0 cents)

beta: ¹¹√ ³⁄₂ (63.8 cents)

gamma: ²⁰√ ³⁄₂ (35.1 cents)

Alpha and Beta may be heard on the title track of her 1986 album Beauty in the Beast.

Proportions between semitone and whole tone

In this section, semitone and whole tone may not have their usual 12-EDO meanings, as it discusses how they may be tempered in different ways from their just versions to produce desired relationships. Let the number of steps in a semitone be s, and the number of steps in a tone be t.

There is exactly one family of equal temperaments that fixes the semitone to any proper fraction of a whole tone, while keeping the notes in the right order (meaning that, for example, C, D, E, F, and F♯ are in ascending order if they preserve their usual relationships to C). That is, fixing q to a proper fraction in the relationship qs = t also defines a unique family of one equal temperament and its multiples that fulfill this relationship.

For example, where k is an integer, 12k-EDO sets q =  ¹⁄₂, and 19k-EDO sets q =  ¹⁄₃. The smallest multiples in these families (e.g. 12 and 19 above) has the additional property of having no notes outside the circle of fifths. (This is not true in general; in 24-EDO, the half-sharps and half-flats are not in the circle of fifths generated starting from C.) The extreme cases are 5k-EDO, where q = 0 and the semitone becomes a unison, and 7k-EDO, where q = 1 and the semitone and tone are the same interval.

Once one knows how many steps a semitone and a tone are in this equal temperament, one can find the number of steps it has in the octave. An equal temperament fulfilling the above properties (including having no notes outside the circle of fifths) divides the octave into 7t − 2s steps, and the perfect fifth into 4t − s steps. If there are notes outside the circle of fifths, one must then multiply these results by n, which is the number of nonoverlapping circles of fifths required to generate all the notes (e.g. two in 24-EDO, six in 72-EDO). (One must take the small semitone for this purpose: 19-EDO has two semitones, one being  ¹⁄₃ tone and the other being  ²⁄₃.)

The smallest of these families is 12k-EDO, and in particular 12-EDO is the smallest equal temperament that has the above properties. Additionally, it also makes the semitone exactly half a whole tone, the simplest possible relationship. These are some of the reasons why 12-EDO has become the most commonly used equal temperament. (Another reason is that 12-EDO is the smallest equal temperament to closely approximate 5-limit harmony, the next-smallest being 19-EDO.)

Each choice of fraction q for the relationship results in exactly one equal temperament family, but the converse is not true: 47-EDO has two different semitones, where one is  ¹⁄₇ tone and the other is  ⁸⁄₉, which are not complements of each other like in 19-EDO ( ¹⁄₃ and  ²⁄₃). Taking each semitone results in a different choice of perfect fifth.

Regular diatonic tunings

The diatonic tuning in twelve equal can be generalized to any regular diatonic tuning dividing the octave as a sequence of steps TTSTTTS (or a rotation of it) with all the T's and all the S's the same size and the S's smaller than the T's. In twelve equal the S is the semitone and is exactly half the size of the tone T. When the S's reduce to zero the result is TTTTT or a five tone equal temperament, As the semitones get larger, eventually the steps are all the same size, and the result is in seven tone equal temperament. These two end points are not included as regular diatonic tunings.

The notes in a regular diatonic tuning are connected together by a cycle of seven tempered fifths. The twelve tone system similarly generalizes to a sequence CDCDDCDCDCDD (or a rotation of it) of chromatic and diatonic semitones connected together in a cycle of twelve fifths. In this case, seven equal is obtained in the limit as the size of C tends to zero and five equal is the limit as D tends to zero while twelve equal is of course the case C = D.

Some of the intermediate sizes of tones and semitones can also be generated in equal temperament systems. For instance if the diatonic semitone is double the size of the chromatic semitone, i.e. D = 2*C the result is nineteen equal with one step for the chromatic semitone, two steps for the diatonic semitone and three steps for the tone and the total number of steps 5*T + 2*S = 15 + 4 = 19 steps. The resulting twelve tone system closely approximates to the historically important 1/3 comma meantone.

If the chromatic semitone is two thirds of the size of the diatonic semitone, i.e. C = (2/3)*D, the result is thirty one equal, with two steps for the chromatic semitone, three steps for the diatonic semitone, and five steps for the tone where 5*T + 2*S = 25 + 6 = 31 steps. The resulting twelve tone system closely approximates to the historically important 1/4 comma meantone.