Rahul Sharma (Editor)

3 3 duoprism

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
3-3 duoprism

In geometry of 4 dimensions, a 3-3 duoprism, the smallest p-q duoprism, is a 4-polytope resulting from the Cartesian product of two triangles.

Contents

It has 9 vertices, 18 edges, 15 faces (9 squares, and 6 triangles), in 6 triangular prism cells. It has Coxeter diagram , and symmetry [[3,2,3]], order 72.

Symmetry

In 5-dimensions, the some uniform 5-polytopes have 3-3 duoprism vertex figures, some with unequal edge-lengths and therefore lower symmetry:

The birectified 16-cell honeycomb also has a 3-3 duoprism vertex figures. There are three constructions for the honeycomb with two lower symmetries.

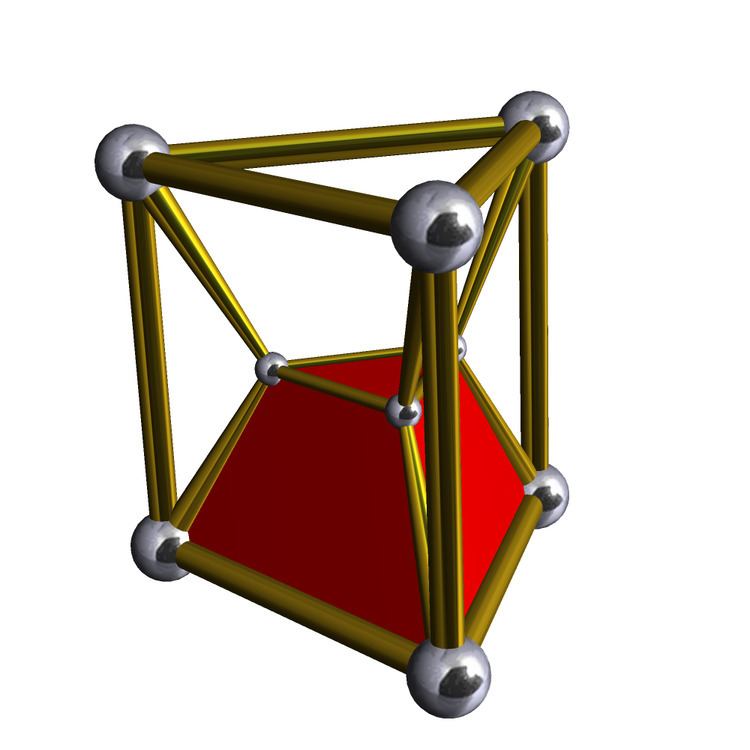
The regular complex polytope 3{4}2, , in C 2 has a real representation as a 3-3 duoprism in 4-dimensional space. 3{4}2 has 9 vertices, and 6 3-edges. Its symmetry is 3[4]2, order 18. It also has a lower symmetry construction, , or 3{}×3{}, with symmetry 3[2]3, order 9. This is the symmetry if the red and blue 3-edges are considered distinct.

3-3 duopyramid

The dual of a 3-3 duoprism is called a 3-3 duopyramid. It has 9 tetragonal disphenoid cells, 18 triangular faces, 15 edges, and 6 vertices.

It can be seen in orthogonal projection as a 6-gon circle of vertices, and edges connecting all pairs, just like a 5-simplex seen in projection.


orthogonal projection

The regular complex polygon 2{4}3 has 6 vertices in C 2 with a real represention in R 4 matching the same vertex arrangement of the 3-3 duopyramid. It has 9 2-edges corresponding to the connecting edges of the 3-3 duopyramid, while the 6 edges connecting the two triangles are not included. It can be seen in a hexagonal projection with 3 sets of colored edges. This arrangement of vertices and edges makes a complete bipartite graph with each vertex from one triangle is connected to every vertex on the other. It is also called a Thomsen graph or 4-cage.

References

3-3 duoprism Wikipedia
(Text) CC BY-SA