Zyablov bound

Statement of the bound

Let R be the rate of the outer code C o u t and δ be the relative distance, then the rate of the concatenated codes satisfies the following bound.

where r is the rate of the inner code C i n .

Description

Let C o u t be the outer code, C i n be the inner code.

Consider C o u t meets the Singleton bound with rate of R , i.e. C o u t has relative distance δ > 1 − R . In order for C o u t ∘ C i n to be an asymptotically good code, C i n also needs to be an asymptotically good code which means, C i n needs to have rate r > 0 and relative distance δ i n > 0 .

Suppose C i n meets the Gilbert-Varshamov bound with rate of r and thus with relative distance

then C o u t ∘ C i n has rate of r R and δ = ( 1 − R ) ( H q − 1 ( 1 − r ) − ε ) .

Expressing R as a function of δ , r

Then optimizing over the choice of r, we get that rate of the Concatenated error correction code satisfies,

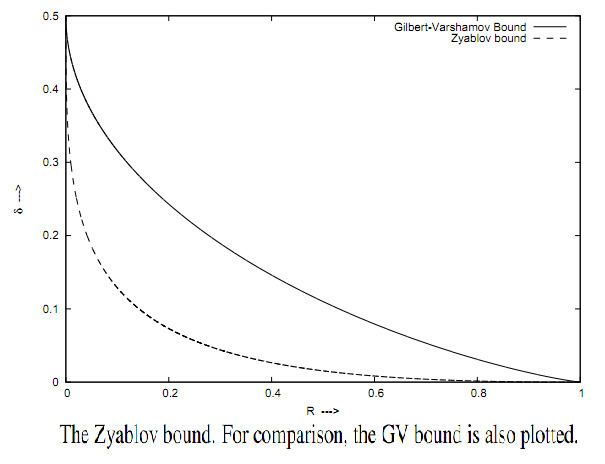
This lower bound is called Zyablov bound (the bound of r < 1 − H q ( δ + ε ) is necessary to ensure R > 0 ). See Figure 2 for a plot of this bound.

Note that the Zyablov bound implies that for every δ > 0 , there exists a (concatenated) code with rate R > 0.

Remarks

We can construct a code that achieves the Zyablov bound in polynomial time. In particular, we can construct explicit asymptotically good code (over some alphabets) in polynomial time.

Linear Codes will help us complete the proof of the above statement since linear codes have polynomial representation. Let Cout be an [ N , K ] Q Reed-Solomon error correction code where N = Q − 1 (evaluation points being F Q ∗ with Q = q k , then k = θ ( log ⁡ N ) .

We need to construct the Inner code that lies on Gilbert-Varshamov bound. This can be done in two ways

1. To perform an exhaustive search on all generator matrices until the required property is satisfied for C i n . This is because Varshamovs bound states that there exists a linear code that lies on Gilbert-Varshamon bound which will take q O ( k n ) time. Using k = r n we get q O ( k n ) = q O ( k 2 ) = N O ( log ⁡ N ) , which is upper bounded by n N O ( log ⁡ n N ) , a quasi-polynomial time bound.

1. To construct C i n in q O ( n ) time and use ( n N ) O ( 1 ) time overall. This can be achieved by using the method of conditional expectation on the proof that random linear code lies on the bound with high probability.

Thus we can construct a code that achieves the Zyablov bound in polynomial time.