 | ||
The zero-velocity surface is a concept that relates to the N-body problem of gravity. It represents a surface a body of given energy cannot cross, since it would have zero velocity on the surface. It was first introduced by George William Hill. The zero-velocity surface is particularly significant when working with weak gravitational interactions among orbiting bodies.
Contents
Three-body problem
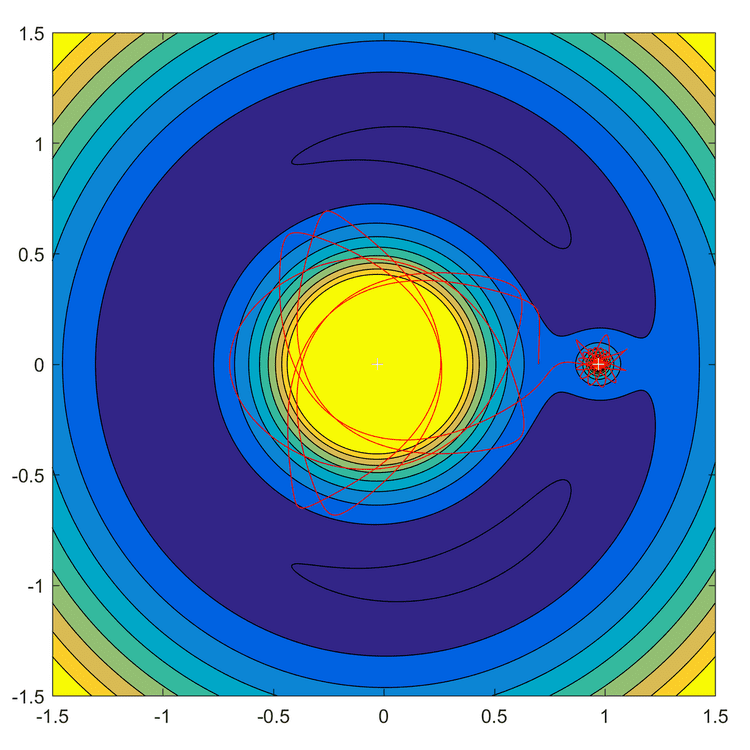
In the circular restricted three-body problem two heavy masses orbit each other at constant radial distance and angular velocity, and a particle of negligible mass is affected by their gravity. By shifting to a rotating coordinate system where the masses are stationary a centrifugal force is introduced. Energy and momentum are not conserved separately in this coordinate system, but the Jacobi integral remains constant:
where
For a given value of
require that
Note that this means zero velocity in the rotating frame: in a non-rotating frame the particle is seen as rotating with the other bodies. The surface also only predicts what regions cannot be entered, not the shape of the trajectory within the surface.
Generalizations
The concept can be generalized to more complex problems, for example with masses in elliptic orbits, the general planar three-body problem, the four-body problem with solar wind drag, or in rings.
Lagrange points
The zero-velocity surface is also an important parameter in finding Lagrange points. These points correspond to locations where the apparent potential in the rotating coordinate system is extremal. This corresponds to places where the zero-velocity surfaces pinch and develop holes as
Galaxy clusters
Given a group of galaxies which are gravitationally interacting, the zero-velocity surface is used to determine which objects are gravitationally bound (i.e. not overcome by the Hubble expansion) and thus part of a galaxy cluster, such as the Local Group.
