Wythoff symbol - Alchetron, The Free Social Encyclopedia

In geometry, the Wythoff symbol represents a Wythoff construction of a uniform polyhedron or plane tiling, from a Schwarz triangle. It was first used by Coxeter, Longuet-Higgins and Miller in their enumeration of the uniform polyhedra.

A Wythoff symbol consists of three numbers and a vertical bar. It represents one uniform polyhedron or tiling, although the same tiling/polyhedron can have different Wythoff symbols from different symmetry generators. For example, the regular cube can be represented by 3 | 4 2 with O_h symmetry, and 2 4 | 2 as a square prism with 2 colors and D_4h symmetry, as well as 2 2 2 | with 3 colors and D 2 h symmetry.

With a slight extension, Wythoff's symbol can be applied to all uniform polyhedra. However, the construction methods do not lead to all uniform tilings in euclidean or hyperbolic space.

Description

In three dimensions, Wythoff's construction begins by choosing a generator point on the triangle. If the distance of this point from each of the sides is non-zero, the point must be chosen to be an equal distance from each edge. A perpendicular line is then dropped between the generator point and every face that it does not lie on.

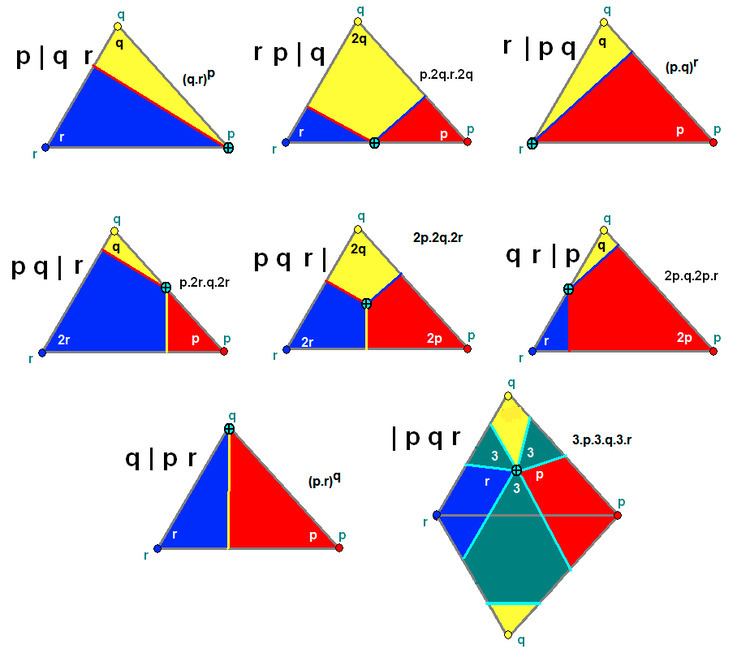
The three numbers in Wythoff's symbol, p , q and r , represent the corners of the Schwarz triangle used in the construction, which are π / p , π / q and π / r radians respectively. The triangle is also represented with the same numbers, written ( p q r ) . The vertical bar in the symbol specifies a categorical position of the generator point within the fundamental triangle according to the following:

p | q r indicates that the generator lies on the corner p ,

p q | r indicates that the generator lies on the edge between p and q ,

p q r | indicates that the generator lies in the interior of the triangle.

In this notation the mirrors are labeled by the reflection-order of the opposite vertex. The p , q , r values are listed before the bar if the corresponding mirror is active.

The one impossible symbol | p q r implies the generator point is on all mirrors, which is only possible if the triangle is degenerate, reduced to a point. This unused symbol is therefore arbitrarily reassigned to represent the case where all mirrors are active, but odd-numbered reflected images are ignored. The resulting figure has rotational symmetry only.

The generator point can either be on or off each mirror, activated or not. This distinction creates 8 (2³) possible forms, neglecting one where the generator point is on all the mirrors.

The Wythoff symbol is functionally similar to the more general Coxeter-Dynkin diagram, in which each node represents a mirror and the arcs between them – marked with numbers – the angles between the mirrors. (An arc representing a right angle is omitted.) A node is circled if the generator point is not on the mirror.

Summary table

There are seven generator points with each set of p , q , r (and a few special forms):

There are three special cases:

p q ( r s ) | – This is a mixture of p q r | and p q s | .

| p q r – Snub forms (alternated) are given by this otherwise unused symbol.

| p q r s – A unique snub form for U75 that isn't Wythoff-constructible.

Symmetry triangles

There are 4 symmetry classes of reflection on the sphere, and two in the Euclidean plane. A few of the infinitely many such patterns in the hyperbolic plane are also listed. (Increasing any of the numbers defining a hyperbolic or Euclidean tiling makes another hyperbolic tiling.)

Point groups:

(p 2 2) dihedral symmetry, p = 2 , 3 , 4 … (order 4 p )

(3 3 2) tetrahedral symmetry (order 24)

(4 3 2) octahedral symmetry (order 48)

(5 3 2) icosahedral symmetry (order 120)

Euclidean (affine) groups:

(4 4 2) *442 symmetry: 45°-45°-90° triangle

(6 3 2) *632 symmetry: 30°-60°-90° triangle

(3 3 3) *333 symmetry (60°-60°-60° plane)

Hyperbolic groups:

(7 3 2) *732 symmetry

(8 3 2) *832 symmetry

(4 3 3) *433 symmetry

(4 4 3) *443 symmetry

(4 4 4) *444 symmetry

(5 4 2) *542 symmetry

(6 4 2) *642 symmetry

The above symmetry groups only include the integer solutions on the sphere. The list of Schwarz triangles includes rational numbers, and determine the full set of solutions of nonconvex uniform polyhedra.

In the tilings above, each triangle is a fundamental domain, colored by even and odd reflections.

Summary spherical, Euclidean and hyperbolic tilings

Selected tilings created by the Wythoff construction are given below.

Some overlapping spherical tilings (r = 2)

For a more complete list, including cases where r ≠ 2, see List of uniform polyhedra by Schwarz triangle.

Tilings are shown as polyhedra. Some of the forms are degenerate, given with brackets for vertex figures, with overlapping edges or vertices.

Dihedral symmetry (q = r = 2)

Spherical tilings with dihedral symmetry exist for all p = 2 , 3 , 4 , … many with digon faces which become degenerate polyhedra. Two of the eight forms (Rectified and cantillated) are replications and are skipped in the table.

Euclidean and hyperbolic tilings (r = 2)

Some representative hyperbolic tilings are given, and shown as a Poincaré disk projection.

Euclidean and hyperbolic tilings (r > 2)

The Coxeter–Dynkin diagram is given in a linear form, although it is actually a triangle, with the trailing segment r connecting to the first node.

References

Wythoff symbol Wikipedia

(Text) CC BY-SA

Contents