Trisha Shetty (Editor)

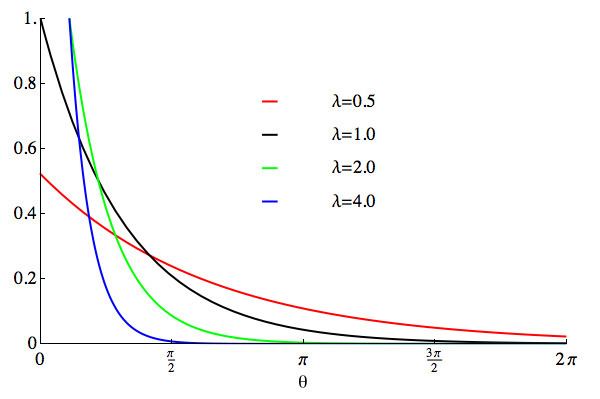
Wrapped exponential distribution

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Wrapped exponential distribution

Parameters
  
λ > 0 {\displaystyle \lambda >0}

Support
  
0 ≤ θ < 2 π {\displaystyle 0\leq \theta <2\pi }

PDF
  
λ e − λ θ 1 − e − 2 π λ {\displaystyle {\frac {\lambda e^{-\lambda \theta }}{1-e^{-2\pi \lambda }}}}

CDF
  
1 − e − λ θ 1 − e − 2 π λ {\displaystyle {\frac {1-e^{-\lambda \theta }}{1-e^{-2\pi \lambda }}}}

Mean
  
arctan ⁡ ( 1 / λ ) {\displaystyle \arctan(1/\lambda )} (circular)

Variance
  
1 − λ 1 + λ 2 {\displaystyle 1-{\frac {\lambda }{\sqrt {1+\lambda ^{2}}}}} (circular)

In probability theory and directional statistics, a wrapped exponential distribution is a wrapped probability distribution that results from the "wrapping" of the exponential distribution around the unit circle.

Contents

Definition

The probability density function of the wrapped exponential distribution is

f W E ( θ ; λ ) = ∑ k = 0 ∞ λ e − λ ( θ + 2 π k ) = λ e − λ θ 1 − e − 2 π λ ,

for 0 ≤ θ < 2 π where λ > 0 is the rate parameter of the unwrapped distribution. This is identical to the truncated distribution obtained by restricting observed values X from the exponential distribution with rate parameter λ to the range 0 ≤ X < 2 π .

Characteristic function

The characteristic function of the wrapped exponential is just the characteristic function of the exponential function evaluated at integer arguments:

φ n ( λ ) = 1 1 − i n / λ

which yields an alternate expression for the wrapped exponential PDF in terms of the circular variable z=e i (θ-m) valid for all real θ and m:

f W E ( z ; λ ) = 1 2 π ∑ n = − ∞ ∞ z − n 1 − i n / λ = { λ π Im ( Φ ( z , 1 , − i λ ) ) − 1 2 π if  z ≠ 1 λ 1 − e − 2 π λ if  z = 1

where Φ ( ) is the Lerch transcendent function.

Circular moments

In terms of the circular variable z = e i θ the circular moments of the wrapped exponential distribution are the characteristic function of the exponential distribution evaluated at integer arguments:

⟨ z n ⟩ = ∫ Γ e i n θ f W E ( θ ; λ ) d θ = 1 1 − i n / λ ,

where Γ is some interval of length 2 π . The first moment is then the average value of z, also known as the mean resultant, or mean resultant vector:

⟨ z ⟩ = 1 1 − i / λ .

The mean angle is

⟨ θ ⟩ = A r g ⟨ z ⟩ = arctan ⁡ ( 1 / λ ) ,

and the length of the mean resultant is

R = | ⟨ z ⟩ | = λ 1 + λ 2 .

and the variance is then 1-R.

Characterisation

The wrapped exponential distribution is the maximum entropy probability distribution for distributions restricted to the range 0 ≤ θ < 2 π for a fixed value of the expectation E ⁡ ( θ ) .

References

Wrapped exponential distribution Wikipedia
(Text) CC BY-SA