 | ||
In his book A New Kind of Science, Stephen Wolfram described a universal 2-state 5-color Turing machine, and conjectured that a particular 2-state 3-symbol Turing machine (hereinafter (2,3) Turing machine) might be universal as well.
Contents
On May 14, 2007, Wolfram announced a $25,000 prize to be won by the first person to prove or disprove the universality of the (2,3) Turing machine. On 24 October 2007, it was announced that the prize had been won by Alex Smith, a student in electronics and computing at the University of Birmingham, for his proof that it was universal, though the proof was initially disputed.
Description
The following table indicates the actions to be performed by the Turing machine depending on whether its current state is A or B, and the symbol currently being read is 0, 1 or 2. The table entries indicate the symbol to be printed, the direction in which the tape head is to move, and the subsequent state of the machine.
The (2,3) Turing machine:
Minsky (1967) briefly argues that standard (2,2) machines cannot be universal; thus, it might seem that the (2,3) Turing machine would be the smallest possible universal Turing machine (in terms of number of states times number of symbols). However, the results are not directly comparable, because Minsky only considers machines that explicitly halt, which the (2,3) machine does not. More generally, almost all formal definitions of Turing machines differ in details irrelevant to their power, but perhaps relevant to what can be expressed using a given number of states and symbols; there is no single standard formal definition. The (2,3) Turing machine also requires an infinite non-repeating input, again making a direct comparison to earlier small Turing machines problematic.
Therefore, though it may be true that the (2,3) machine is in some sense the "smallest possible universal Turing machine", this has not been strictly proven, and the claim is open to debate.
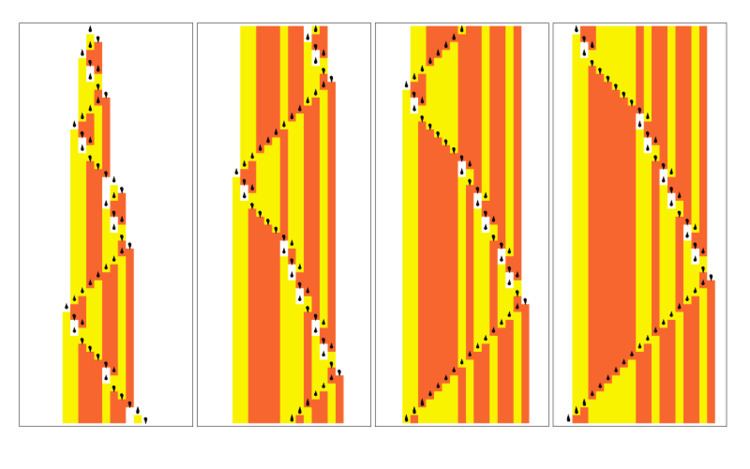
The state of the head (up or down droplet (A and B respectively)) and the pattern of color (white, yellow and orange (0,1, and 2 respectively)) in a given row depends solely on the content of the row immediately above it.
Even though the machine has a head with only two states, and a tape that can hold only three colors (depending on the initial content of the tape), the machine's output can still be remarkably complex.
Proof of universality
On 24 October 2007, it was announced by Wolfram Research that Alex Smith, a student in electronics and computing at the University of Birmingham (UK), proved that the (2,3) Turing machine is universal and thus won Wolfram's prize described above.
The proof showed that the machine is equivalent to a variant of a tag system already known to be universal. Smith first constructed a sequence of rule systems showing that the (2,3) Turing machine is capable of arbitrary finite computations. He then employed a novel approach to extend that construction to unbounded computations. The proof proceeds in two stages. The first part emulates the finite evolution of any two-color cyclic tag system. The emulation is a composite of a series of emulations involving the indexed rule systems 'system 0' through 'system 5'. Each rule system emulates the next one in the sequence. Smith then showed that even though the initial condition of the (2,3) Turing machine is not repetitive, the construction of that initial condition is not universal. Hence the (2,3) Turing machine is universal.
Wolfram claims that Smith's proof is another piece of evidence for Wolfram's general Principle of Computational Equivalence (PCE). That principle states that if one sees behavior that is not obviously simple, the behavior will correspond to a computation that is in a sense “maximally sophisticated”. Smith's proof has unleashed a debate on the precise operational conditions a Turing machine must satisfy in order for it to be candidate universal machine.
A universal (2,3) Turing machine has conceivable applications. For instance, a machine that small and simple can be embedded or constructed using a small number of particles or molecules. But the “compiler” Smith's algorithm implies does not produce compact or efficient code, at least for anything but the simplest cases. Hence the resulting code tends to be astronomically large and very inefficient. Whether there exist more efficient codings enabling the (2,3) Turing machine to compute more rapidly is an open question.
Dispute
The announcement that Alex Smith's proof had won was made without the approval of the judging committee, as noted by Martin Davis, a member of the committee, in a post to the FOM mailing list:
"As far as I know, no member of the committee has passed on the validity of this 40 page proof. The determination that Smith's proof is correct seems to have been made entirely by the Wolfram organization. My understanding is that the I/O involves complex encodings."Vaughan Pratt subsequently disputed the correctness of this proof in a public list of discussion, noting that similar techniques would allow a linear bounded automaton (or LBA) to be universal, which would contradict a known non-universality result due to Noam Chomsky. Alex Smith joined the mailing list after this message and replied on the following day explaining that a LBA would require to be restarted manually to become universal using the same initial configuration, while his construction restarts the Turing machine automatically with no external intervention. Discussions about the proof continued for some time between Alex Smith, Vaughan Pratt, and others.
