 | ||
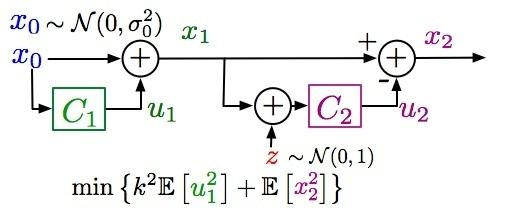
Witsenhausen's counterexample, shown in the figure below, is a deceptively simple toy problem in decentralized stochastic control. It was formulated by Hans Witsenhausen in 1968. It is a counterexample to a natural conjecture that one can generalize a key result of centralized linear–quadratic–Gaussian control systems—that in a system with linear dynamics, Gaussian disturbance, and quadratic cost, affine (linear) control laws are optimal—to decentralized systems. Witsenhausen constructed a two-stage linear quadratic Gaussian system where two decisions are made by decision makers with decentralized information and showed that for this system, there exist nonlinear control laws that outperform all linear laws. The problem of finding the optimal control law remains unsolved.
Contents
Statement of the counterexample
The statement of the counterexample is simple: two controllers attempt to control the system by attempting to bring the state close to zero in exactly two time steps. The first controller observes the initial state
with the second controller's observation equation
The objective is to minimize an expected cost function,
where the expectation is taken over the randomness in the initial state
The problem is to find control functions
that give at least as good a value of the objective function as do any other pair of control functions. Witsenhausen showed that the optimal functions
Specific results of Witsenhausen
Witsenhausen obtained the following results:
The significance of the problem
The counterexample lies at the intersection of control theory and information theory. Due to its hardness, the problem of finding the optimal control law has also received attention from the theoretical computer science community. The importance of the problem was reflected upon in the 47th IEEE Conference on Decision and Control (CDC) 2008, Cancun, Mexico, where an entire session was dedicated to understanding the counterexample 40 years after it was first formulated.
The problem is of conceptual significance in decentralized control because it shows that it is important for the controllers to communicate with each other implicitly in order to minimize the cost. This suggests that control actions in decentralized control may have a dual role: those of control and communication.
The hardness of the problem
The hardness of the problem is attributed to the fact that information of the second controller depends on the decisions of the first controller. Variations considered by Tamer Basar show that the hardness is also because of the structure of the performance index and the coupling of different decision variables. It has also been shown that problems of the spirit of Witsenhausen's counterexample become simpler if the transmission delay along an external channel that connects the controllers is smaller than the propagation delay in the problem. However, this result requires the channels to be perfect and instantaneous, and hence is of limited applicability. In practical situations, the channel is always imperfect, and thus one can not assume that decentralized control problems are simple in presence of external channels.
A justification of the failure of attempts that discretize the problem came from the computer science literature: Christos Papadimitriou and John Tsitsiklis showed that the discrete version of the counterexample is NP-complete.
Attempts at obtaining a solution
A number of numerical attempts have been made to solve the counterexample. Focusing on a particular choice of problem parameters
