Weyr canonical form

Definition

A basic Weyr matrix with eigenvalue λ is an n × n matrix W of the following form: There is a partition

such that, when W is viewed as an r × r blocked matrix ( W i j ) , where the ( i , j ) block W i j is an n i × n j matrix, the following three features are present:

1. The main diagonal blocks W i i are the n i × n i scalar matrices λ I for i = 1 , … , r .
2. The first superdiagonal blocks W i , i + 1 are full column rank n i × n i + 1 matrices in reduced row-echelon form (that is, an identity matrix followed by zero rows) for i = 1 , … , r − 1 .
3. All other blocks of W are zero (that is, W i j = 0 when j ≠ i , i + 1 ).

In this case, we say that W has Weyr structure ( n 1 , n 2 , … , n r ) .

Example

The following is an example of a basic Weyr matrix.

In this matrix, n = 9 and n 1 = 4 , n 2 = 2 , n 3 = 2 , n 4 = 1 . So W has the Weyr structure ( 4 , 2 , 2 , 1 ) . Also,

and

Definition

Let W be a square matrix and let λ 1 , … , λ k be the distinct eigenvalues of W . We say that W is in Weyr form (or is a Weyr matrix) if W has the following form:

where W i is a basic Weyr matrix with eigenvalue λ i for i = 1 , … , k .

Example

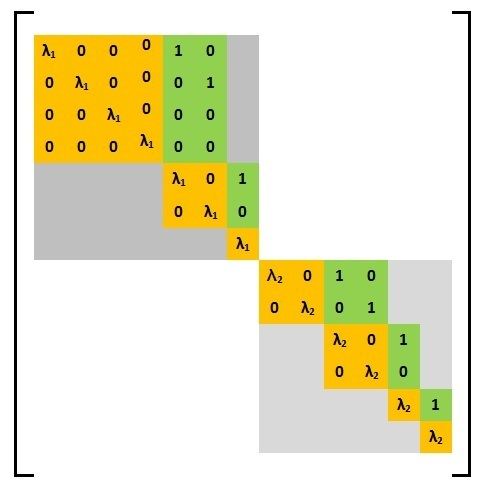
The following image shows an example of a general Weyr matrix consisting of three basic Weyr matrix blocks. The basic Weyr matrix in the top-left corner has the structure (4,2,1) with eigenvalue 4, the middle block has structure (2,2,1,1) with eigenvalue -3 and the one in the lower-right corner has the structure (3, 2) with eigenvalue 0.

The Weyr form is canonical

That the Weyr form is a canonical form of a matrix is a consequence of the following result: Each square matrix A over an algebraically closed field is similar to a Weyr matrix W which is unique up to permutation of its basic blocks. The matrix W is called the Weyr (canonical) form of A .

Reduction to the nilpotent case

Let A be a square matrix of order n over an algebraically closed field and let the distinct eigenvalues of A be λ 1 , λ 2 , … , λ k . As a consequence of the generalized eigenspace decomposition theorem, one can show that A is similar to a block diagonal matrix of the form

A = [ λ 1 I + N 1 λ 2 I + N 2 ⋱ λ k I + N k ] = [ λ 1 I λ 2 I ⋱ λ k I ] + [ N 1 N 2 ⋱ N k ] = D + N

where D is a diagonal matrix and N is a nilpotent matrix. So the problem of reducing A to the Weyr form reduces to the problem of reducing the nilpotent matrices N i to the Weyr form.

Reduction of a nilpotent matrix to the Weyr form

Given a nilpotent square matrix A of order n over an algebraically closed field F , the following algorithm produces an invertible matrix C and a Weyr matrix W such that W = C − 1 A C .

Step 1

Let A 1 = A

Step 2

1. Compute a basis for the null space of A 1 .
2. Extend the basis for the null space of A 1 to a basis for the n -dimensional vector space F n .
3. Form the matrix P 1 consisting of these basis vectors.
4. Compute P 1 − 1 A 1 P 1 = [ 0 B 2 0 A 2 ] . A 2 is a square matrix of size n − nullity ( A 1 ) .

Step 3

If A 2 is nonzero, repeat Step 2 on A 2 .

1. Compute a basis for the null space of A 2 .
2. Extend the basis for the null space of A 2 to a basis for the vector space having dimension n − nullity ( A 1 ) .
3. Form the matrix P 2 consisting of these basis vectors.
4. Compute P 2 − 1 A 2 P 2 = [ 0 B 3 0 A 3 ] . A 2 is a square matrix of size n − nullity ( A 1 ) − nullity ( A 2 ) .

Step 4

Continue the processes of Steps 1 and 2 to obtain increasingly smaller square matrices A 1 , A 2 , A 3 , … and associated nvertible matrices P 1 , P 2 , P 3 , … until the first zero matrix A r is obtained.

Step 5

The Weyr structure of A is ( n 1 , n 2 , … , n r ) where n i = nullity ( A i ) .

Step 6

1. Compute the matrix P = P 1 [ I 0 0 P 2 ] [ I 0 0 P 3 ] ⋯ [ I 0 0 P r ] (here the I 's are appropriately sized identity matrices).
2. Compute X = P − 1 A P . X is a matrix of the following form:

Step 7

Use elementary row operations to find an invertible matrix Y r − 1 of appropriate size such that the product Y r − 1 X r , r − 1 is a matrix of the form I r , r − 1 = [ I O ] .

Step 8

Set Q 1 = diag ( I , I , … , Y r − 1 − 1 , I ) and compute Q 1 − 1 X Q 1 . In this matrix, the ( r , r − 1 ) -block is I r , r − 1 .

Step 9

Find a matrix R 1 formed as a product of elementary matrices such that R 1 − 1 Q 1 − 1 X Q 1 R 1 is a matrix in which all the blocks above the block I r , r − 1 contain only 0 's.

Step 10

Repeat Steps 8 and 9 on column r − 1 converting ( r − 1 , r − 2 ) -block to I r − 1 , r − 2 via conjugation by some invertible matrix Q 2 . Use this block to clear out the blocks above, via conjugation by a product R 2 of elementary matrices.

Step 11

Repeat these processes on r − 2 , r − 3 , … , 3 , 2 columns, using conjugations by Q 3 , R 3 , … , Q r − 2 , R r − 2 , Q r − 1 . The resulting matrix W is now in Weyr form.

Step 12

Let C = P 1 diag ( I , P 2 ) ⋯ diag ( I , P r − 1 ) Q 1 R 1 Q 2 ⋯ R r − 2 Q r − 1 . Then W = C − 1 A C .

Applications of the Weyr form

Some well-known applications of the Weyr form are listed below:

1. The Weyr form can be used to simplify the proof of Gerstenhaber’s Theorem which asserts that the subalgebra generated by two commuting n × n matrices has dimension at most n .
2. A set of finite matrices is said to be approximately simultaneously diagonalizable if they can be perturbed to simultaneously diagonalizable matrices. The Weyr form is used to prove approximate simultaneous diagonalizability of various classes of matrices. The approximate simultaneous diagonalizability property has applications in the study of phylogenetic invariants in biomathematics.
3. The Weyr form can be used to simplify the proofs of the irreducibility of the variety of all k-tuples of commuting complex matrices.