Von Mises yield criterion - Alchetron, the free social encyclopedia

The von Mises yield criterion suggests that the yielding of materials begins when the second deviatoric stress invariant J 2 reaches a critical value. It is part of a plasticity theory that applies best to ductile materials, such as metals. Prior to yield, material response can be assumed to be anything i.e. nonlinear elastic, viscoelastic or simply linear elastic.

In materials science and engineering the von Mises yield criterion can be also formulated in terms of the von Mises stress or equivalent tensile stress, σ v , a scalar stress value that can be computed from the Cauchy stress tensor. In this case, a material is said to start yielding when its von Mises stress reaches a critical value known as the yield strength, σ y . The von Mises stress is used to predict yielding of materials under any loading condition from results of simple uniaxial tensile tests. The von Mises stress satisfies the property that two stress states with equal distortion energy have equal von Mises stress.

Because the von Mises yield criterion is independent of the first stress invariant, I 1 , it is applicable for the analysis of plastic deformation for ductile materials such as metals, as the onset of yield for these materials does not depend on the hydrostatic component of the stress tensor.

Although formulated by James Clerk Maxwell in 1865, it is generally attributed to Richard Edler von Mises (1913). Tytus Maksymilian Huber (1904), in a paper in Polish, anticipated to some extent this criterion. This criterion is also referred to as the Maxwell–Huber–Hencky–von Mises theory.

Mathematical formulation

Mathematically the von Mises yield criterion is expressed as:

J 2 = k 2

where k is the yield stress of the material in pure shear. As shown later in this article, at the onset of yielding, the magnitude of the shear yield stress in pure shear is (√3)times lower than the tensile yield stress in the case of simple tension. Thus, we have:

k = σ y 3

where σ y is the yield strength of the material. If we set the von Mises stress equal to the yield strength and combine the above equations, the von Mises yield criterion can be expressed as:

σ v = σ y = 3 J 2

or

σ v 2 = 3 J 2 = 3 k 2

Substituting J 2 with terms of the Cauchy stress tensor components

σ v 2 = 1 2 [ ( σ 11 − σ 22 ) 2 + ( σ 22 − σ 33 ) 2 + ( σ 33 − σ 11 ) 2 + 6 ( σ 23 2 + σ 31 2 + σ 12 2 ) ]

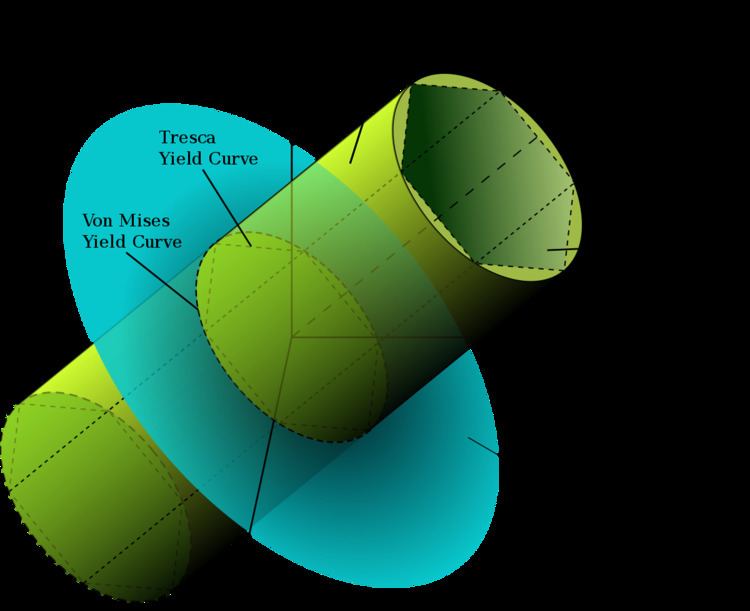
This equation defines the yield surface as a circular cylinder (See Figure) whose yield curve, or intersection with the deviatoric plane, is a circle with radius 2 k , or 2 3 σ y . This implies that the yield condition is independent of hydrostatic stresses.

Reduced von Mises equation for different stress conditions

The above equation can be reduced and reorganized for practical use in different loading scenarios.

In the case of uniaxial stress or simple tension, σ 1 ≠ 0 , σ 3 = σ 2 = 0 , the von Mises criterion simply reduces to

σ 1 = σ y ,

which means the material starts to yield when σ 1 reaches the yield strength of the material σ y , and is in agreement with the definition of tensile (or compressive) yield strength.

It is also convenient to define an Equivalent tensile stress or von Mises stress, σ v , which is used to predict yielding of materials under multiaxial loading conditions using results from simple uniaxial tensile tests. Thus, we define

σ v = 3 J 2 = ( σ 11 − σ 22 ) 2 + ( σ 22 − σ 33 ) 2 + ( σ 33 − σ 11 ) 2 + 6 ( σ 12 2 + σ 23 2 + σ 31 2 ) 2 = ( σ 1 − σ 2 ) 2 + ( σ 2 − σ 3 ) 2 + ( σ 3 − σ 1 ) 2 2 = 3 2 s i j s i j

where s i j are the components of the stress deviator tensor σ d e v :

σ d e v = σ − 1 3 ( tr σ ) I .

In this case, yielding occurs when the equivalent stress, σ v , reaches the yield strength of the material in simple tension, σ y . As an example, the stress state of a steel beam in compression differs from the stress state of a steel axle under torsion, even if both specimens are of the same material. In view of the stress tensor, which fully describes the stress state, this difference manifests in six degrees of freedom, because the stress tensor has six independent components. Therefore, it is difficult to tell which of the two specimens is closer to the yield point or has even reached it. However, by means of the von Mises yield criterion, which depends solely on the value of the scalar von Mises stress, i.e., one degree of freedom, this comparison is straightforward: A larger von Mises value implies that the material is closer to the yield point.

In the case of pure shear stress, σ 12 = σ 21 ≠ 0 , while all other σ i j = 0 , von Mises criterion becomes:

σ 12 = k = σ y 3 .

This means that, at the onset of yielding, the magnitude of the shear stress in pure shear is 3 times lower than the tensile stress in the case of simple tension. The von Mises yield criterion for pure shear stress, expressed in principal stresses, is

( σ 1 − σ 2 ) 2 + ( σ 2 − σ 3 ) 2 + ( σ 1 − σ 3 ) 2 = 2 σ y 2

In the case of plane stress, σ 3 = 0 , the von Mises criterion becomes:

σ 1 2 − σ 1 σ 2 + σ 2 2 = 3 k 2 = σ y 2

This equation represents an ellipse in the plane σ 1 − σ 2 , as shown in the Figure above.

The following table summarizes von Mises yield criterion for the different stress conditions.

Notes:

Subscripts 1,2,3 can be replaced with x,y,z, or other orthogonal coordinate system

Shear stress is denoted here as σ i j ; in practice it is also denoted as τ i j

Physical interpretation of the von Mises yield criterion

Hencky (1924) offered a physical interpretation of von Mises criterion suggesting that yielding begins when the elastic energy of distortion reaches a critical value. For this reason, the von Mises criterion is also known as the maximum distortion strain energy criterion. This comes from the relation between J 2 and the elastic strain energy of distortion W D :

W D = J 2 2 G with the elastic shear modulus G = E 2 ( 1 + ν ) .

In 1937 Arpad L. Nadai suggested that yielding begins when the octahedral shear stress reaches a critical value, i.e. the octahedral shear stress of the material at yield in simple tension. In this case, the von Mises yield criterion is also known as the maximum octahedral shear stress criterion in view of the direct proportionality that exists between J 2 and the octahedral shear stress, τ o c t , which by definition is

τ o c t = 2 3 J 2

thus we have

τ o c t = 2 3 σ y

Practical engineering usage of the von Mises yield criterion

Use of the von Mises Criterion as a failure theory is only exactly applicable when homogeneous material properties are equal to

F s y F t y = 1 3 = 0.577

Since no material will have this ratio precisely, in practice it is necessary to use engineering judgement to decide what failure theory is appropriate for a given material. Alternately, for use of the Tresca Theory, the same ratio is defined as 1/2.

The yield Margin of safety is written as

M S y l d = F y σ v − 1

Although the given criterion is based on a yield phenomenon, extensive testing has shown that use of a "von Mises" stress is applicable at ultimate loading

M S u l t = F u σ v − 1

Comparison with Tresca yield criterion

Also shown in the figure is Tresca's maximum shear stress criterion (dashed line). Observe that Tresca's yield surface is circumscribed by von Mises's. Therefore, it predicts plastic yielding already for stress states that are still elastic according to the von Mises criterion. As a model for plastic material behavior, Tresca's criterion is therefore more conservative, but not more accurate depending on the applicability for a given material.

References

Von Mises yield criterion Wikipedia

(Text) CC BY-SA