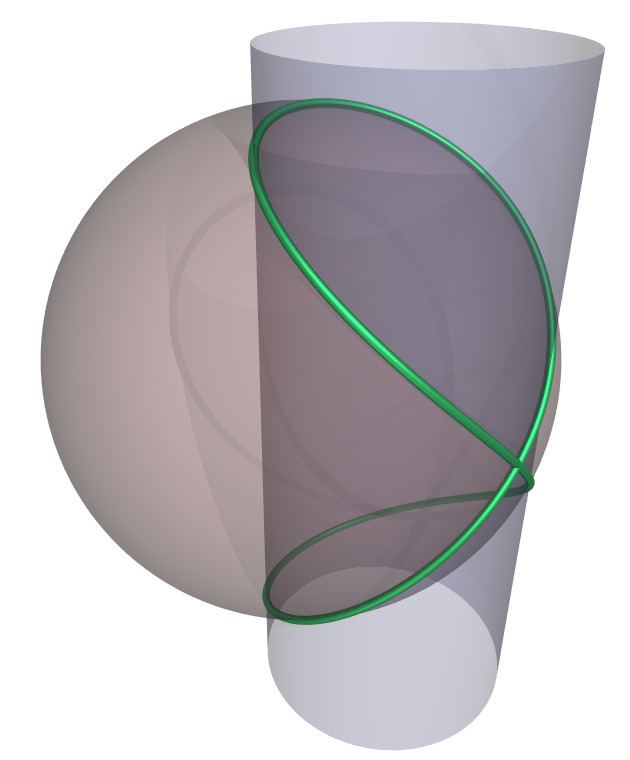
Viviani's curve - Alchetron, The Free Social Encyclopedia

In mathematics, particularly geometry, Viviani's curve, also known as Viviani's window, is a figure eight shaped space curve named after the Italian mathematician Vincenzo Viviani, the intersection of a sphere with a cylinder that is tangent to the sphere and passes through the center of the sphere.

The projection of Viviani's curve onto a plane perpendicular to the line through the crossing point and the sphere center is the lemniscate of Gerono.

Formula

The curve can be obtained by intersecting a sphere of radius 2 a centered at the origin,

x 2 + y 2 + z 2 = 4 a 2

with the cylinder centered at ( a , 0 , 0 ) of radius a given by

( x − a ) 2 + y 2 = a 2 .

The resulting curve of intersection, V , can be parameterized by t to give the parametric equation of Viviani's curve:

V ( t ) = ⟨ a ( 1 + cos ⁡ ( t ) ) , a sin ⁡ ( t ) , 2 a sin ⁡ ( t 2 ) ⟩ .

This is a clelie with m = 1 , where θ = t − π 2 .

References

Viviani's curve Wikipedia

(Text) CC BY-SA