 | ||
In geometry and physics, the versor of an axis or of a vector is a unit vector indicating its direction.
Contents
The versor of a Cartesian axis is also known as a standard basis vector. The versor of a vector is also known as a normalized vector.
Versors of a Cartesian coordinate system
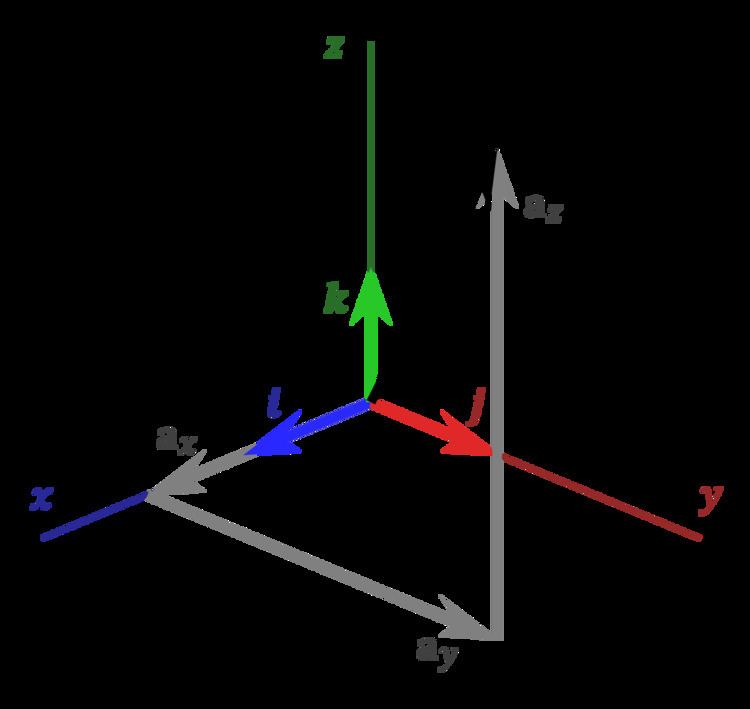
The versors of the axes of a Cartesian coordinate system are the unit vectors codirectional with the axes of that system. Every Euclidean vector a in a n-dimensional Euclidean space (Rn) can be represented as a linear combination of the n versors of the corresponding Cartesian coordinate system. For instance, in a three-dimensional space (R3), there are three versors:
They indicate the direction of the Cartesian axes x, y, and z, respectively. In terms of these, any vector a can be represented as
where ax, ay, az are called the vector components (or vector projections) of a on the Cartesian axes x, y, and z (see figure), while ax, ay, az are the respective scalar components (or scalar projections).
In linear algebra, the set formed by these n versors is typically referred to as the standard basis of the corresponding Euclidean space, and each of them is commonly called a standard basis vector.
Notation
A hat above the symbol of a versor is sometimes used to emphasize its status as a unit vector (e.g.,
In most contexts it can be assumed that i, j, and k, (or
Versor of a non-zero vector
The versor (or normalized vector)
where
