Utility functions on indivisible goods - Alchetron, the free social encyclopedia

Some branches of economics and game theory deal with indivisible goods, discrete items that can be traded only as a whole. For example, in combinatorial auctions there is a finite set of items, and every agent can buy a subset of the items, but an item cannot be divided among two or more agents.

Monotonicity

Monotonicity means that an agent always (weakly) prefers to have extra items. Formally:

For a preference relation: A ⊇ B implies A ⪰ B .

For a utility function: A ⊇ B implies u ( A ) ≥ u ( B ) (i.e. u is a monotone function).

Monotonicity is equivalent to the free disposal assumption: if an agent may always discard unwanted items, then extra items can never decrease the utility.

Additivity

Additivity (also called linearity or modularity) means that "the whole is equal to the sum of its parts." That is, the utility of a set of items is the sum of the utilities of each item separately. This property is relevant only for cardinal utility functions. It says that for every set A of items,

u ( A ) = ∑ x ∈ A u ( x )

assuming that u ( ∅ ) = 0 . In other words, u is an additive function. An equivalent definition is: for any sets of items A and B ,

u ( A ) + u ( B ) = u ( A ∪ B ) + u ( A ∩ B ) .

An additive utility function is characteristic of independent goods. For example, an apple and a hat are considered independent: the utility a person receives from having an apple is the same whether or not he has a hat, and vice versa. A typical utility function for this case is given at the right.

Submodularity and Supermodularity

Submodularity means that "the whole is not more than the sum of its parts (and may be less)." Formally, for all sets A and B ,

u ( A ) + u ( B ) ≥ u ( A ∪ B ) + u ( A ∩ B )

In other words, u is a submodular set function.

An equivalent property is diminishing marginal utility, which means that for any sets A and B with A ⊆ B , and every x ∉ B :

u ( A ∪ { x } ) − u ( A ) ≥ u ( B ∪ { x } ) − u ( B ) .

A submodular utility function is characteristic of substitute goods. For example, an apple and a bread loaf can be considered substitutes: the utility a person receives from eating an apple is smaller if he has already ate bread (and vice versa), since he is less hungry in that case. A typical utility function for this case is given at the right.

Supermodularity is the opposite of submodularity: it means that "the whole is not less than the sum of its parts (and may be more)". Formally, for all sets A and B ,

u ( A ) + u ( B ) ≤ u ( A ∪ B ) + u ( A ∩ B )

In other words, u is a supermodular set function.

An equivalent property is increasing marginal utility, which means that for all sets A and B with A ⊆ B , and every x ∉ B :

u ( B ∪ { x } ) − u ( B ) ≥ u ( A ∪ { x } ) − u ( A ) .

A supermoduler utility function is characteristic of complementary goods. For example, an apple and a knife can be considered complementary: the utility a person receives from an apple is larger if he already has a knife (and vice versa), since it is easier to eat an apple after cutting it with a knife. A possible utility function for this case is given at the right.

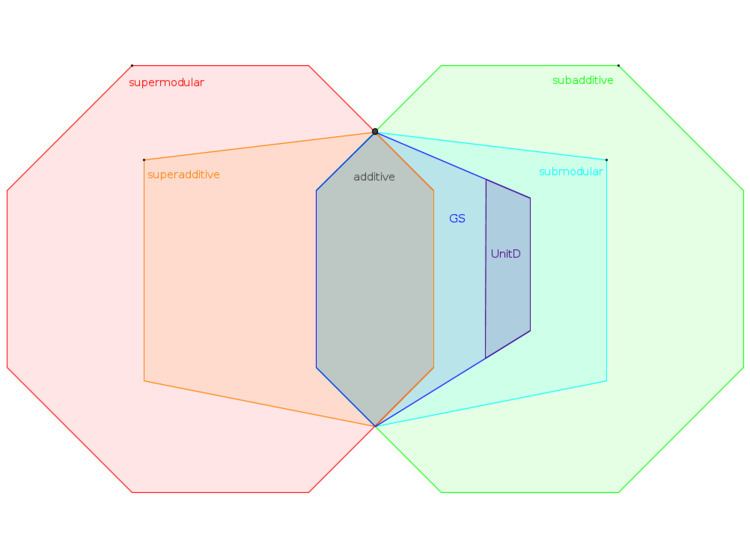
A utility function is additive if and only if it is both submodular and supermodular.

Subadditivity and Superadditivity

Subadditivity means that for every pair of disjoint sets A , B :

In other words, u is a subadditive set function.

Every submodular function is subadditive, but the opposite is not true. For example, assume that there are 3 identical items, X Y and Z, and the utility depends only on their quantity. The table on the right describes a utility function that is subadditive but not submodular, since:

Superadditivity is the opposite of subadditivity and means that for every pair of disjoint sets A , B :

In other words, u is a superadditive set function.

Every superadditive function is supermodular.

A utility function is additive if and only if it is both superadditive and subadditive.

Unit demand

Unit demand (UD) means that the agent only wants a single good. If the agent gets two or more goods, he uses the one of them that gives him the highest utility, and discards the rest. Formally:

For a preference relation: for every set B there is a subset A ⊆ B with cardinality | A | = 1 , such that A ⪰ B .

For a utility function: For every set A :

u ( A ) = max x ∈ A u ( x )

A unit-demand function is an extreme case of a submodular function. It is characteristic of goods that are pure substitutes. For example, if there are an apple and a pear, and an agent wants to eat a single fruit, then his utility function is unit-demand, as exemplified in the table at the right.

Gross substitutes

Gross substitutes (GS) means that the agents regards the items as substitute goods or independent goods but not complementary goods. There are many formal definitions to this property, all of which are equivalent.

Every UD valuation is GS, but the opposite is not true.

Every GS valuation is submodular, but the opposite is not true.

See Gross substitutes (indivisible items) for more details.

Hence the following relations hold between the classes:

U D ⊊ G S ⊊ S u b m o d u l a r ⊊ S u b a d d i t i v e

See diagram on the right.

Aggregates of utility functions

A utility function describes the happiness of an individual. Often, we need a function that describes the happiness of an entire society. Such a function is called a Social welfare function, and it is usually an aggregate function of two or more utility functions. If the individual utility functions are additive, then the following is true for the aggregate functions:

References

Utility functions on indivisible goods Wikipedia

(Text) CC BY-SA

Contents