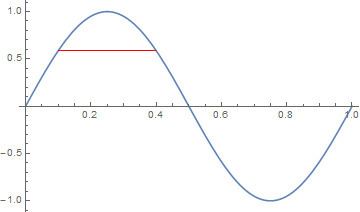
In mathematical analysis, the universal chord theorem states that if a function f is continuous on [a,b] and satisfies f ( a ) = f ( b ) , then for every natural number n , there exists some x ∈ [ a , b ] such that f ( x ) = f ( x + 1 n ) .
The theorem was published by Paul Lévy in 1934 as a generalization of Rolle's Theorem.
Let H ( f ) = { h ∈ [ 0 , 1 ] : f ( x ) = f ( x + h ) for some x } denote the chord set of the function f. If f is a continuous function and h ∈ H ( f ) , then h n ∈ H ( f ) for all natural numbers n.
The case when n = 2 can be considered an application of the Borsuk–Ulam theorem to the real line. It says that if f ( x ) is continuous on some interval I = [ a , b ] with the condition that f ( a ) = f ( b ) , then there exists some x ∈ [ a , b ] such that f ( x ) = f ( x + 1 / 2 ) .
In less generality, if f : [ 0 , 1 ] → R is continuous and f ( 0 ) = f ( 1 ) , then there exists x ∈ [ 0 , 1 2 ] that satisfies f ( x ) = f ( x + 1 / 2 ) .