Uncertainty theory

Four axioms

Axiom 1. (Normality Axiom) M { Γ } = 1  for the universal set  Γ .

Axiom 2. (Self-Duality Axiom) M { Λ } + M { Λ c } = 1  for any event  Λ .

Axiom 3. (Countable Subadditivity Axiom) For every countable sequence of events Λ₁, Λ₂, ..., we have

Axiom 4. (Product Measure Axiom) Let ( Γ k , L k , M k ) be uncertainty spaces for k = 1 , 2 , ⋯ , n . Then the product uncertain measure M is an uncertain measure on the product σ-algebra satisfying

Principle. (Maximum Uncertainty Principle) For any event, if there are multiple reasonable values that an uncertain measure may take, then the value as close to 0.5 as possible is assigned to the event.

Uncertain variables

An uncertain variable is a measurable function ξ from an uncertainty space ( Γ , L , M ) to the set of real numbers, i.e., for any Borel set B of real numbers, the set { ξ ∈ B } = { γ ∈ Γ | ξ ( γ ) ∈ B } is an event.

Uncertainty distribution

Uncertainty distribution is inducted to describe uncertain variables.

Definition:The uncertainty distribution Φ ( x ) : R → [ 0 , 1 ] of an uncertain variable ξ is defined by Φ ( x ) = M { ξ ≤ x } .

Theorem(Peng and Iwamura, Sufficient and Necessary Condition for Uncertainty Distribution) A function Φ ( x ) : R → [ 0 , 1 ] is an uncertain distribution if and only if it is an increasing function except Φ ( x ) ≡ 0 and Φ ( x ) ≡ 1 .

Independence

Definition: The uncertain variables ξ 1 , ξ 2 , … , ξ m are said to be independent if

for any Borel sets B 1 , B 2 , … , B m of real numbers.

Theorem 1: The uncertain variables ξ 1 , ξ 2 , … , ξ m are independent if

for any Borel sets B 1 , B 2 , … , B m of real numbers.

Theorem 2: Let ξ 1 , ξ 2 , … , ξ m be independent uncertain variables, and f 1 , f 2 , … , f m measurable functions. Then f 1 ( ξ 1 ) , f 2 ( ξ 2 ) , … , f m ( ξ m ) are independent uncertain variables.

Theorem 3: Let Φ i be uncertainty distributions of independent uncertain variables ξ i , i = 1 , 2 , … , m respectively, and Φ the joint uncertainty distribution of uncertain vector ( ξ 1 , ξ 2 , … , ξ m ) . If ξ 1 , ξ 2 , … , ξ m are independent, then we have

for any real numbers x 1 , x 2 , … , x m .

Operational law

Theorem: Let ξ 1 , ξ 2 , … , ξ m be independent uncertain variables, and f : R n → R a measurable function. Then ξ = f ( ξ 1 , ξ 2 , … , ξ m ) is an uncertain variable such that

where B , B 1 , B 2 , … , B m are Borel sets, and f ( B 1 , B 2 , … , B m ) ⊂ B means f ( x 1 , x 2 , … , x m ) ∈ B for any x 1 ∈ B 1 , x 2 ∈ B 2 , … , x m ∈ B m .

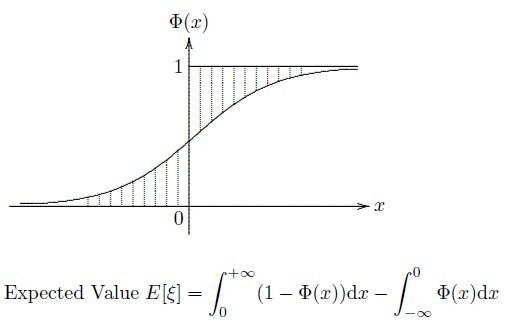
Expected Value

Definition: Let ξ be an uncertain variable. Then the expected value of ξ is defined by

provided that at least one of the two integrals is finite.

Theorem 1: Let ξ be an uncertain variable with uncertainty distribution Φ . If the expected value exists, then

Theorem 2: Let ξ be an uncertain variable with regular uncertainty distribution Φ . If the expected value exists, then

Theorem 3: Let ξ and η be independent uncertain variables with finite expected values. Then for any real numbers a and b , we have

Variance

Definition: Let ξ be an uncertain variable with finite expected value e . Then the variance of ξ is defined by

Theorem: If ξ be an uncertain variable with finite expected value, a and b are real numbers, then

Critical value

Definition: Let ξ be an uncertain variable, and α ∈ ( 0 , 1 ] . Then

is called the α-optimistic value to ξ , and

is called the α-pessimistic value to ξ .

Theorem 1: Let ξ be an uncertain variable with regular uncertainty distribution Φ . Then its α-optimistic value and α-pessimistic value are

Theorem 2: Let ξ be an uncertain variable, and α ∈ ( 0 , 1 ] . Then we have

Theorem 3: Suppose that ξ and η are independent uncertain variables, and α ∈ ( 0 , 1 ] . Then we have

( ξ + η ) s u p ( α ) = ξ s u p ( α ) + η s u p α ,

( ξ + η ) i n f ( α ) = ξ i n f ( α ) + η i n f α ,

( ξ ∨ η ) s u p ( α ) = ξ s u p ( α ) ∨ η s u p α ,

( ξ ∨ η ) i n f ( α ) = ξ i n f ( α ) ∨ η i n f α ,

( ξ ∧ η ) s u p ( α ) = ξ s u p ( α ) ∧ η s u p α ,

( ξ ∧ η ) i n f ( α ) = ξ i n f ( α ) ∧ η i n f α .

Entropy

Definition: Let ξ be an uncertain variable with uncertainty distribution Φ . Then its entropy is defined by

where S ( x ) = − t ln ( t ) − ( 1 − t ) ln ( 1 − t ) .

Theorem 1(Dai and Chen): Let ξ be an uncertain variable with regular uncertainty distribution Φ . Then

Theorem 2: Let ξ and η be independent uncertain variables. Then for any real numbers a and b , we have

Theorem 3: Let ξ be an uncertain variable whose uncertainty distribution is arbitrary but the expected value e and variance σ 2 . Then

Inequalities

Theorem 1(Liu, Markov Inequality): Let ξ be an uncertain variable. Then for any given numbers t > 0 and p > 0 , we have

Theorem 2 (Liu, Chebyshev Inequality) Let ξ be an uncertain variable whose variance V [ ξ ] exists. Then for any given number t > 0 , we have

Theorem 3 (Liu, Holder’s Inequality) Let p and q be positive numbers with 1 / p + 1 / q = 1 , and let ξ and η be independent uncertain variables with E [ | ξ | p ] < ∞ and E [ | η | q ] < ∞ . Then we have

Theorem 4:(Liu [127], Minkowski Inequality) Let p be a real number with p ≤ 1 , and let ξ and η be independent uncertain variables with E [ | ξ | p ] < ∞ and E [ | η | q ] < ∞ . Then we have

Convergence concept

Definition 1: Suppose that ξ , ξ 1 , ξ 2 , … are uncertain variables defined on the uncertainty space ( Γ , L , M ) . The sequence { ξ i } is said to be convergent a.s. to ξ if there exists an event Λ with M { Λ } = 1 such that

for every γ ∈ Λ . In that case we write ξ i → ξ ,a.s.

Definition 2: Suppose that ξ , ξ 1 , ξ 2 , … are uncertain variables. We say that the sequence { ξ i } converges in measure to ξ if

for every ε > 0 .

Definition 3: Suppose that ξ , ξ 1 , ξ 2 , … are uncertain variables with finite expected values. We say that the sequence { ξ i } converges in mean to ξ if

Definition 4: Suppose that Φ , ϕ 1 , Φ 2 , … are uncertainty distributions of uncertain variables ξ , ξ 1 , ξ 2 , … , respectively. We say that the sequence { ξ i } converges in distribution to ξ if Φ i → Φ at any continuity point of Φ .

Theorem 1: Convergence in Mean ⇒ Convergence in Measure ⇒ Convergence in Distribution. However, Convergence in Mean ⇎ Convergence Almost Surely ⇎ Convergence in Distribution.

Conditional uncertainty

Definition 1: Let ( Γ , L , M ) be an uncertainty space, and A , B ∈ L . Then the conditional uncertain measure of A given B is defined by

Theorem 1: Let ( Γ , L , M ) be an uncertainty space, and B an event with M { B } > 0 . Then M{·|B} defined by Definition 1 is an uncertain measure, and ( Γ , L , M { · | B } ) is an uncertainty space.

Definition 2: Let ξ be an uncertain variable on ( Γ , L , M ) . A conditional uncertain variable of ξ given B is a measurable function ξ | B from the conditional uncertainty space ( Γ , L , M { · | B } ) to the set of real numbers such that

Definition 3: The conditional uncertainty distribution Φ → [ 0 , 1 ] of an uncertain variable ξ given B is defined by

provided that M { B } > 0 .

Theorem 2: Let ξ be an uncertain variable with regular uncertainty distribution Φ ( x ) , and t a real number with Φ ( t ) < 1 . Then the conditional uncertainty distribution of ξ given ξ > t is

Theorem 3: Let ξ be an uncertain variable with regular uncertainty distribution Φ ( x ) , and t a real number with Φ ( t ) > 0 . Then the conditional uncertainty distribution of ξ given ξ ≤ t is

Definition 4: Let ξ be an uncertain variable. Then the conditional expected value of ξ given B is defined by

provided that at least one of the two integrals is finite.