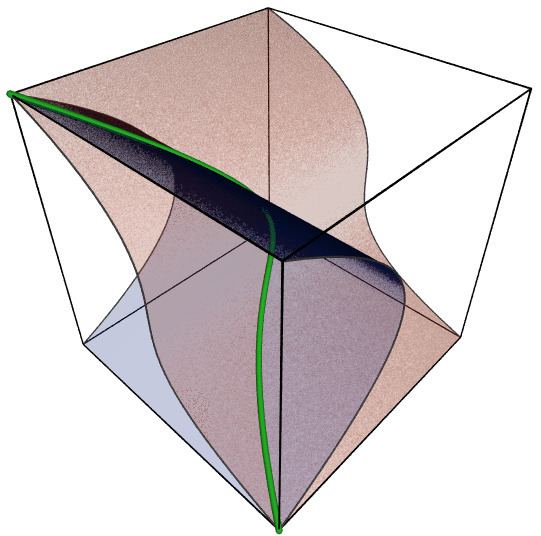
Twisted cubic - Alchetron, The Free Social Encyclopedia

In mathematics, a twisted cubic is a smooth, rational curve C of degree three in projective 3-space P³. It is a fundamental example of a skew curve. It is essentially unique, up to projective transformation (the twisted cubic, therefore). It is generally considered to be the simplest example of a projective variety that is not linear or a hypersurface, and is given as such in most textbooks on algebraic geometry. It is the three-dimensional case of the rational normal curve, and is the image of a Veronese map of degree three on the projective line.

Definition

It is most easily given parametrically as the image of the map

ν : P 1 → P 3

which assigns to the homogeneous coordinate [ S : T ] the value

ν : [ S : T ] ↦ [ S 3 : S 2 T : S T 2 : T 3 ] .

In one coordinate patch of projective space, the map is simply the moment curve

ν : x ↦ ( x , x 2 , x 3 )

That is, it is the closure by a single point at infinity of the affine curve ( x , x 2 , x 3 ) .

Equivalently, it is a projective variety, defined as the zero locus of three smooth quadrics. Given the homogeneous coordinates [X:Y:Z:W] on P³, it is the zero locus of the three homogeneous polynomials

F 0 = X Z − Y 2 F 1 = Y W − Z 2 F 2 = X W − Y Z .

It may be checked that these three quadratic forms vanish identically when using the explicit parameterization above; that is, substituting x³ for X, and so on.

In fact, the homogeneous ideal of the twisted cubic C is generated by three algebraic forms of degree two on P³. The generators of the ideal are

{ X Z − Y 2 , Y W − Z 2 , X W − Y Z } .

Properties

The twisted cubic has an assortment of elementary properties:

It is the set-theoretic complete intersection of XZ-Y² and Z ( Y W − Z 2 ) − W ( X W − Y Z ) , but not a scheme-theoretic or ideal-theoretic complete intersection (the resulting ideal is not radical, since ( Y W − Z 2 ) 2 is in it, but Y W − Z 2 is not).

Any four points on C span P³.

Given six points in P³ with no four coplanar, there is a unique twisted cubic passing through them.

The union of the tangent and secant lines, the secant variety, of a twisted cubic C fill up P³ and the lines are pairwise disjoint, except at points of the curve itself. In fact, the union of the tangent and secant lines of any non-planar smooth algebraic curve is three-dimensional. Further, any smooth algebraic variety with the property that every length four subscheme spans P³ has the property that the tangent and secant lines are pairwise disjoint, except at points of the variety itself.

The projection of C onto a plane from a point on a tangent line of C yields a cuspidal cubic.

The projection from a point on a secant line of C yields a nodal cubic.

The projection from a point on C yields a conic section.

References

Twisted cubic Wikipedia

(Text) CC BY-SA

Contents

Definition

Properties

References