 | ||
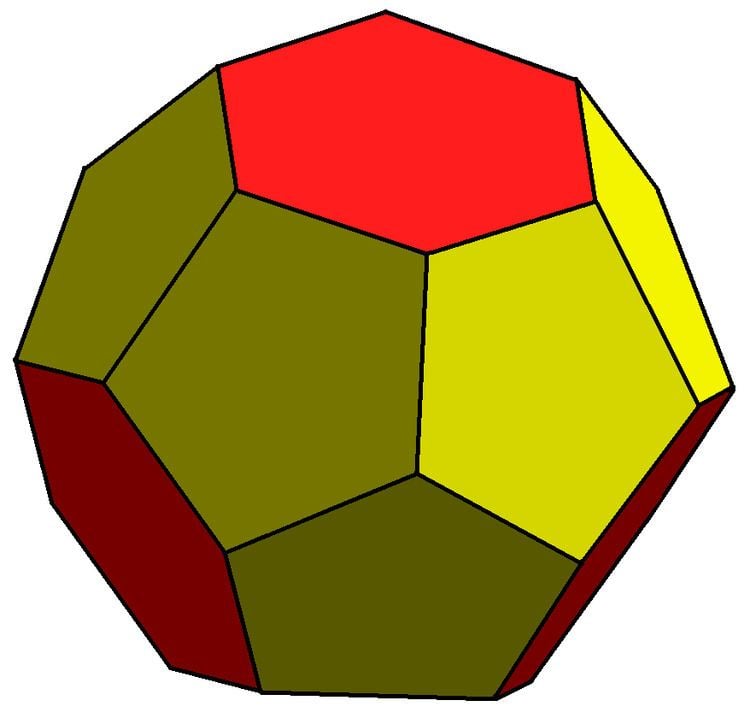
The truncated triakis tetrahedron is a convex polyhedron with 16 faces: 4 sets of 3 pentagons arranged in a tetrahedral arrangement, with 4 hexagons in the gaps. It is constructed from taking a triakis tetrahedron by truncating the order-6 vertices. This creates 4 regular hexagon faces, and leaves 12 irregular pentagons.
A topologically similar equilateral polyhedron can be constructed by using 12 regular pentagons with 4 equilateral but nonplanar hexagons, each vertex with internal angles alternating between 108 and 132 degrees.
Full truncation
If all of a triakis tetrahedron's vertices, of both kinds, are truncated, the resulting solid is an irregular icosahedron, whose dual is a trihexakis truncated tetrahedron.
Truncation of only the simpler vertices yields what looks like a tetrahedron with each face raised by a low triangular frustum. The dual to that truncation will be the triakis truncated tetrahedron.
