 | ||
Tropical geometry is a relatively new area in mathematics, which might loosely be described as a piece-wise linear or skeletonized version of algebraic geometry. Its leading ideas had appeared in different forms in the earlier works of George M. Bergman and of Robert Bieri and John Groves, but only since the late 1990s has an effort been made to consolidate the basic definitions of the theory. This has been motivated by the applications to enumerative algebraic geometry found by Grigory Mikhalkin.
Contents
History of the name
The adjective tropical in the name of the area was coined by French mathematicians in honor of the Hungarian-born Brazilian mathematician Imre Simon, who wrote on the field. Jean-Eric Pin attributes the coinage to Dominique Perrin, whereas Simon himself attributes the word to Christian Choffrut.
Basic definitions
We will use the min convention, that tropical addition is classical minimum. It is also possible to cast the whole subject in terms of the max convention, negating throughout, and several authors make this choice. The basic ideas of tropical analysis have been developed independently in the same notations by mathematicians working in various fields (see and references therein). In 1987 V. P. Maslov introduced a tropical version of integration procedure. He also noticed that the Legendre transformation and solutions of the Hamilton-Jacobi equation are linear operations in the tropical sense.
The tropical semiring (also known as a tropical algebra or, with the max convention, the max-plus algebra, due to the name of its operations) is a semiring (ℝ ∪ {∞}, ⊕, ⊗), with the operations as follows:
Tropical exponentiation is defined in the usual way as iterated tropical products (see exponentiation#In abstract algebra).
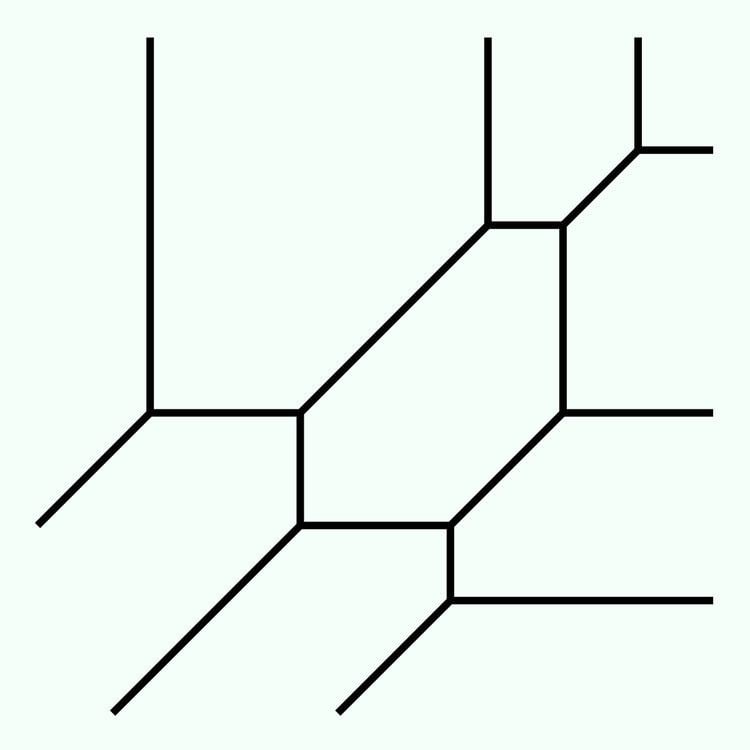
A monomial of variables in this semiring is a linear map, represented in classical arithmetic as a linear function of the variables with integer coefficients. A polynomial in the semiring is the minimum of a finite number of such monomials, and is therefore a concave, continuous, piecewise linear function.
The set of points where a tropical polynomial F is non-differentiable is called its associated tropical hypersurface.
There are two important characterizations of these objects:
- Tropical hypersurfaces are exactly the rational polyhedral complexes satisfying a "zero-tension" condition.
- Tropical surfaces are exactly the non-Archimedean amoebas over an algebraically closed non-Archimedean field K.
These two characterizations provide a "dictionary" between combinatorics and algebra. Such a dictionary can be used to take an algebraic problem and solve its easier combinatorial counterpart instead.
The tropical hypersurface can be generalized to a tropical variety by taking the non-Archimedean amoeba of ideals I in K[x1, ..., xn] instead of polynomials. The tropical variety of an ideal I equals the intersection of the tropical hypersurfaces associated to every polynomial in I. This intersection can be chosen to be finite.
There are a number of articles and surveys on tropical geometry. The study of tropical curves (tropical hypersurfaces in ℝ2) is particularly well developed. In fact, for this setting, mathematicians have established analogues of many classical theorems; e.g., Pappus's hexagon theorem, Bézout's theorem, the degree-genus formula, and the group law of the cubics all have tropical counterparts.
Applications
Tropical geometry was used by economist Paul Klemperer to design auctions used by the Bank of England during the financial crisis in 2007. Shiozawa defined subtropical algebra as max-times or min-times semiring (instead of max-plus and min-plus). He found that Ricardian trade theory (international trade without input trade) can be interpreted as subtropical convex algebra. Moreover, several optimization problems arising for instance in job scheduling, location analysis, transportation networks, decision making and discrete event dynamical systems can be formulated and solved in the framework of tropical geometry. A tropical counterpart of Abel-Jacobi map can be applied to a crystal design. The weights in a weighted finite-state transducer are often required to be a tropical semiring.
