Trigonometric constants expressed in real radicals

Scope of this article

The list in this article is incomplete in several senses. First, the trigonometric functions of all angles that are integer multiples of those given can also be expressed in radicals, but some are omitted here.

Second, it is always possible to apply the half-angle formula to find an expression in radicals for a trigonometric function of one-half of any angle on the list, then half of that angle, etc.

Third, expressions in real radicals exist for a trigonometric function of a rational multiple of π if and only if the denominator of the fully reduced rational multiple is a power of 2 by itself or the product of a power of 2 with the product of distinct Fermat primes, of which the known ones are 3, 5, 17, 257, and 65537. This article only gives the cases based on the Fermat primes 3 and 5. Thus for example cos(2π/17), given in the article 17-gon, is not given here.

Fourth, this article only deals with trigonometric function values when the expression in radicals is in real radicals—roots of real numbers. Many other trigonometric function values are expressible in, for example, cube roots of complex numbers that cannot be rewritten in terms of roots of real numbers. For example, the trigonometric function values of any angle that is one-third of an angle θ considered in this article can be expressed in cube roots and square roots by using the cubic equation formula to solve

4 cos 3 ⁡ θ 3 − 3 cos ⁡ θ 3 = cos ⁡ θ ,

but in general the solution for the cosine of the one-third angle involves the cube root of a complex number (giving casus irreducibilis).

In practice, all values of sines, cosines, and tangents not found in this article are approximated using the techniques described at Generating trigonometric tables.

Table of some common angles

Several different units of angle measure are widely used, including degrees, radians, and gradians (gons):

1 full circle (turn) = 360 degrees = 2π radians  =  400 gons.

The following table shows the conversions and values for some common angles:

Further angles

Values outside the [0°, 45°] angle range are trivially derived from these values, using circle axis reflection symmetry. (See Trigonometric identity.)

In the entries below, when a certain number of degrees is related to a regular polygon, the relation is that the number of degrees in each angle of the polygon is (n – 2) times the indicated number of degrees (where n is the number of sides). This is because the sum of the angles of any n-gon is 180° × (n – 2) and so the measure of each angle of any regular n-gon is 180° × (n – 2) ÷ n. Thus for example the entry "45°: square" means that, with n = 4, 180° ÷ n = 45°, and the number of degrees in each angle of a square is (n – 2) × 45° = 90°.

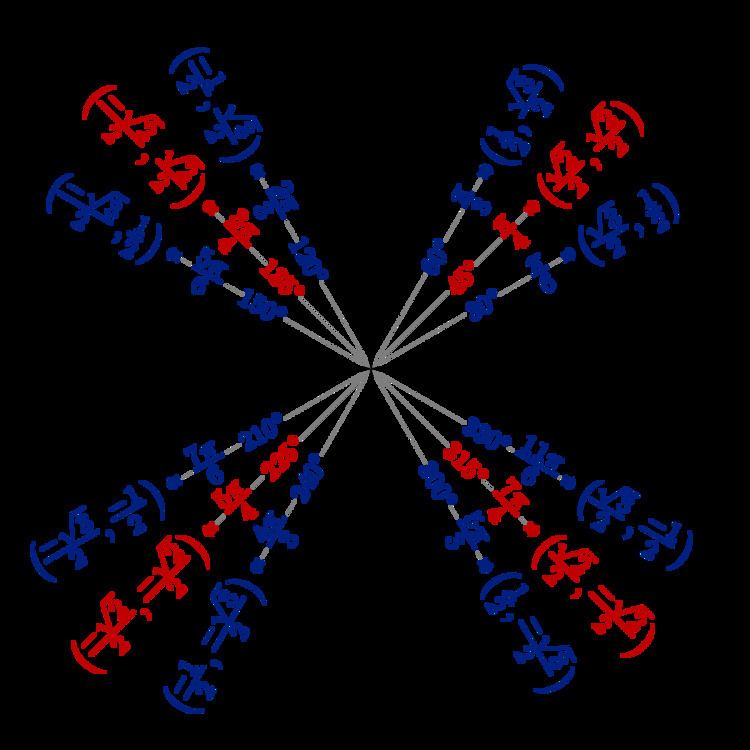
0°: fundamental

sin ⁡ 0 = 0 cos ⁡ 0 = 1 tan ⁡ 0 = 0 cot ⁡ 0  is undefined

1.5°: regular hecatonicosagon (120-sided polygon)

sin ⁡ ( π 120 ) = sin ⁡ ( 1.5 ∘ ) = ( 2 + 2 ) ( 15 + 3 − 10 − 2 5 ) − ( 2 − 2 ) ( 30 − 6 5 + 5 + 1 ) 16 cos ⁡ ( π 120 ) = cos ⁡ ( 1.5 ∘ ) = ( 2 + 2 ) ( 30 − 6 5 + 5 + 1 ) + ( 2 − 2 ) ( 15 + 3 − 10 − 2 5 ) 16

1.875°: regular enneacontahexagon (96-sided polygon)

sin ⁡ ( π 96 ) = sin ⁡ ( 1.875 ∘ ) = 1 2 2 − 2 + 2 + 2 + 3 cos ⁡ ( π 96 ) = cos ⁡ ( 1.875 ∘ ) = 1 2 2 + 2 + 2 + 2 + 3

2.25°: regular octacontagon (80-sided polygon)

sin ⁡ ( π 80 ) = sin ⁡ ( 2.25 ∘ ) = 1 2 2 − 2 + 2 + 5 + 5 2 cos ⁡ ( π 80 ) = cos ⁡ ( 2.25 ∘ ) = 1 2 2 + 2 + 2 + 5 + 5 2

2.8125°: regular hexacontatetragon (64-sided polygon)

sin ⁡ ( π 64 ) = sin ⁡ ( 2.8125 ∘ ) = 1 2 2 − 2 + 2 + 2 + 2 cos ⁡ ( π 64 ) = cos ⁡ ( 2.8125 ∘ ) = 1 2 2 + 2 + 2 + 2 + 2

3°: regular hexacontagon (60-sided polygon)

sin ⁡ ( π 60 ) = sin ⁡ ( 3 ∘ ) = 2 ( 1 − 3 ) 5 + 5 + ( 10 − 2 ) ( 3 + 1 ) 16 cos ⁡ ( π 60 ) = cos ⁡ ( 3 ∘ ) = 2 ( 1 + 3 ) 5 + 5 + ( 10 − 2 ) ( 3 − 1 ) 16 tan ⁡ ( π 60 ) = tan ⁡ ( 3 ∘ ) = [ ( 2 − 3 ) ( 3 + 5 ) − 2 ] [ 2 − 10 − 2 5 ] 4 cot ⁡ ( π 60 ) = cot ⁡ ( 3 ∘ ) = [ ( 2 + 3 ) ( 3 + 5 ) − 2 ] [ 2 + 10 − 2 5 ] 4

3.75°: regular tetracontaoctagon (48-sided polygon)

sin ⁡ ( π 48 ) = sin ⁡ ( 3.75 ∘ ) = 1 2 2 − 2 + 2 + 3 cos ⁡ ( π 48 ) = cos ⁡ ( 3.75 ∘ ) = 1 2 2 + 2 + 2 + 3

4.5°: regular tetracontagon (40-sided polygon)

sin ⁡ ( π 40 ) = sin ⁡ ( 4.5 ∘ ) = 1 2 2 − 2 + 5 + 5 2 cos ⁡ ( π 40 ) = cos ⁡ ( 4.5 ∘ ) = 1 2 2 + 2 + 5 + 5 2

5.625°: regular triacontadigon (32-sided polygon)

sin ⁡ ( π 32 ) = sin ⁡ ( 5.625 ∘ ) = 1 2 2 − 2 + 2 + 2 cos ⁡ ( π 32 ) = cos ⁡ ( 5.625 ∘ ) = 1 2 2 + 2 + 2 + 2

6°: regular triacontagon (30-sided polygon)

sin ⁡ π 30 = sin ⁡ 6 ∘ = 30 − 180 − 5 − 1 8 cos ⁡ π 30 = cos ⁡ 6 ∘ = 10 − 20 + 3 + 15 8 tan ⁡ π 30 = tan ⁡ 6 ∘ = 10 − 20 + 3 − 15 2 cot ⁡ π 30 = cot ⁡ 6 ∘ = 27 + 15 + 50 + 2420 2

7.5°: regular icositetragon (24-sided polygon)

sin ⁡ ( π 24 ) = sin ⁡ ( 7.5 ∘ ) = 1 2 2 − 2 + 3 = 1 4 8 − 2 6 − 2 2 cos ⁡ ( π 24 ) = cos ⁡ ( 7.5 ∘ ) = 1 2 2 + 2 + 3 = 1 4 8 + 2 6 + 2 2 tan ⁡ ( π 24 ) = tan ⁡ ( 7.5 ∘ ) = 6 − 3 + 2 − 2   = ( 2 − 1 ) ( 3 − 2 ) cot ⁡ ( π 24 ) = cot ⁡ ( 7.5 ∘ ) = 6 + 3 + 2 + 2   = ( 2 + 1 ) ( 3 + 2 )

9°: regular icosagon (20-sided polygon)

sin ⁡ π 20 = sin ⁡ 9 ∘ = 1 2 2 − 5 + 5 2 cos ⁡ π 20 = cos ⁡ 9 ∘ = 1 2 2 + 5 + 5 2 tan ⁡ π 20 = tan ⁡ 9 ∘ = 5 + 1 − 5 + 2 5 cot ⁡ π 20 = cot ⁡ 9 ∘ = 5 + 1 + 5 + 2 5

11.25°: regular hexadecagon (16-sided polygon)

sin ⁡ π 16 = sin ⁡ 11.25 ∘ = 1 2 2 − 2 + 2 cos ⁡ π 16 = cos ⁡ 11.25 ∘ = 1 2 2 + 2 + 2 tan ⁡ π 16 = tan ⁡ 11.25 ∘ = 4 + 2 2 − 2 − 1 cot ⁡ π 16 = cot ⁡ 11.25 ∘ = 4 + 2 2 + 2 + 1

12°: regular pentadecagon (15-sided polygon)

sin ⁡ π 15 = sin ⁡ 12 ∘ = 1 8 [ 2 ( 5 + 5 ) + 3 − 15 ] cos ⁡ π 15 = cos ⁡ 12 ∘ = 1 8 [ 6 ( 5 + 5 ) + 5 − 1 ] tan ⁡ π 15 = tan ⁡ 12 ∘ = 1 2 [ 3 3 − 15 − 2 ( 25 − 11 5 ) ] cot ⁡ π 15 = cot ⁡ 12 ∘ = 1 2 [ 15 + 3 + 2 ( 5 + 5 ) ]

15°: regular dodecagon (12-sided polygon)

sin ⁡ π 12 = sin ⁡ 15 ∘ = 1 4 ( 6 − 2 ) = 1 2 2 − 3 cos ⁡ π 12 = cos ⁡ 15 ∘ = 1 4 ( 6 + 2 ) = 1 2 2 + 3 tan ⁡ π 12 = tan ⁡ 15 ∘ = 2 − 3 cot ⁡ π 12 = cot ⁡ 15 ∘ = 2 + 3

18°: regular decagon (10-sided polygon)

sin ⁡ π 10 = sin ⁡ 18 ∘ = 1 4 ( 5 − 1 ) cos ⁡ π 10 = cos ⁡ 18 ∘ = 1 4 2 ( 5 + 5 ) tan ⁡ π 10 = tan ⁡ 18 ∘ = 1 5 5 ( 5 − 2 5 ) cot ⁡ π 10 = cot ⁡ 18 ∘ = 5 + 2 5

21°: sum 9° + 12°

sin ⁡ 7 π 60 = sin ⁡ 21 ∘ = 1 16 ( 2 ( 3 + 1 ) 5 − 5 − ( 6 − 2 ) ( 1 + 5 ) ) cos ⁡ 7 π 60 = cos ⁡ 21 ∘ = 1 16 ( 2 ( 3 − 1 ) 5 − 5 + ( 6 + 2 ) ( 1 + 5 ) ) tan ⁡ 7 π 60 = tan ⁡ 21 ∘ = 1 4 ( 2 − ( 2 + 3 ) ( 3 − 5 ) ) ( 2 − 2 ( 5 + 5 ) ) cot ⁡ 7 π 60 = cot ⁡ 21 ∘ = 1 4 ( 2 − ( 2 − 3 ) ( 3 − 5 ) ) ( 2 + 2 ( 5 + 5 ) )

22.5°: regular octagon

sin ⁡ π 8 = sin ⁡ 22.5 ∘ = 1 2 2 − 2 , cos ⁡ π 8 = cos ⁡ 22.5 ∘ = 1 2 2 + 2 tan ⁡ π 8 = tan ⁡ 22.5 ∘ = 2 − 1 cot ⁡ π 8 = cot ⁡ 22.5 ∘ = 2 + 1 (the silver ratio)

24°: sum 12° + 12°

sin ⁡ 2 π 15 = sin ⁡ 24 ∘ = 1 8 [ 15 + 3 − 2 ( 5 − 5 ) ] cos ⁡ 2 π 15 = cos ⁡ 24 ∘ = 1 8 ( 6 ( 5 − 5 ) + 5 + 1 ) tan ⁡ 2 π 15 = tan ⁡ 24 ∘ = 1 2 [ 50 + 22 5 − 3 3 − 15 ] cot ⁡ 2 π 15 = cot ⁡ 24 ∘ = 1 2 [ 15 − 3 + 2 ( 5 − 5 ) ]

27°: sum 12° + 15°

sin ⁡ 3 π 20 = sin ⁡ 27 ∘ = 1 8 [ 2 5 + 5 − 2 ( 5 − 1 ) ] cos ⁡ 3 π 20 = cos ⁡ 27 ∘ = 1 8 [ 2 5 + 5 + 2 ( 5 − 1 ) ] tan ⁡ 3 π 20 = tan ⁡ 27 ∘ = 5 − 1 − 5 − 2 5 cot ⁡ 3 π 20 = cot ⁡ 27 ∘ = 5 − 1 + 5 − 2 5

30°: regular hexagon

sin ⁡ π 6 = sin ⁡ 30 ∘ = 1 2 cos ⁡ π 6 = cos ⁡ 30 ∘ = 3 2 tan ⁡ π 6 = tan ⁡ 30 ∘ = 3 3 = 1 3 cot ⁡ π 6 = cot ⁡ 30 ∘ = 3

33°: sum 15° + 18°

sin ⁡ 11 π 60 = sin ⁡ 33 ∘ = 1 16 [ 2 ( 3 − 1 ) 5 + 5 + 2 ( 1 + 3 ) ( 5 − 1 ) ] cos ⁡ 11 π 60 = cos ⁡ 33 ∘ = 1 16 [ 2 ( 3 + 1 ) 5 + 5 + 2 ( 1 − 3 ) ( 5 − 1 ) ] tan ⁡ 11 π 60 = tan ⁡ 33 ∘ = 1 4 [ 2 − ( 2 − 3 ) ( 3 + 5 ) ] [ 2 + 2 ( 5 − 5 ) ] cot ⁡ 11 π 60 = cot ⁡ 33 ∘ = 1 4 [ 2 − ( 2 + 3 ) ( 3 + 5 ) ] [ 2 − 2 ( 5 − 5 ) ]

36°: regular pentagon

sin ⁡ π 5 = sin ⁡ 36 ∘ = 1 4 10 − 2 5 cos ⁡ π 5 = cos ⁡ 36 ∘ = 5 + 1 4 = φ 2 , where φ is the golden ratio; tan ⁡ π 5 = tan ⁡ 36 ∘ = 5 − 2 5 cot ⁡ π 5 = cot ⁡ 36 ∘ = 1 5 25 + 10 5

39°: sum 18° + 21°

sin ⁡ 13 π 60 = sin ⁡ 39 ∘ = 1 16 [ 2 ( 1 − 3 ) 5 − 5 + 2 ( 3 + 1 ) ( 5 + 1 ) ] cos ⁡ 13 π 60 = cos ⁡ 39 ∘ = 1 16 [ 2 ( 1 + 3 ) 5 − 5 + 2 ( 3 − 1 ) ( 5 + 1 ) ] tan ⁡ 13 π 60 = tan ⁡ 39 ∘ = 1 4 [ ( 2 − 3 ) ( 3 − 5 ) − 2 ] [ 2 − 2 ( 5 + 5 ) ] cot ⁡ 13 π 60 = cot ⁡ 39 ∘ = 1 4 [ ( 2 + 3 ) ( 3 − 5 ) − 2 ] [ 2 + 2 ( 5 + 5 ) ]

42°: sum 21° + 21°

sin ⁡ 7 π 30 = sin ⁡ 42 ∘ = 30 + 180 − 5 + 1 8 cos ⁡ 7 π 30 = cos ⁡ 42 ∘ = 15 − 3 + 10 + 20 8 tan ⁡ 7 π 30 = tan ⁡ 42 ∘ = 15 + 3 − 10 + 20 2 cot ⁡ 7 π 30 = cot ⁡ 42 ∘ = 50 − 2420 + 27 − 15 2

45°: square

sin ⁡ π 4 = sin ⁡ 45 ∘ = 2 2 = 1 2 cos ⁡ π 4 = cos ⁡ 45 ∘ = 2 2 = 1 2 tan ⁡ π 4 = tan ⁡ 45 ∘ = 1 cot ⁡ π 4 = cot ⁡ 45 ∘ = 1

54°: sum 27° + 27°

sin ⁡ 3 π 10 = sin ⁡ 54 ∘ = 5 + 1 4 cos ⁡ 3 π 10 = cos ⁡ 54 ∘ = 10 − 2 5 4 tan ⁡ 3 π 10 = tan ⁡ 54 ∘ = 25 + 10 5 5 cot ⁡ 3 π 10 = cot ⁡ 54 ∘ = 5 − 20

60°: equilateral triangle

sin ⁡ π 3 = sin ⁡ 60 ∘ = 3 2 cos ⁡ π 3 = cos ⁡ 60 ∘ = 1 2 tan ⁡ π 3 = tan ⁡ 60 ∘ = 3 cot ⁡ π 3 = cot ⁡ 60 ∘ = 3 3 = 1 3

67.5°: sum 7.5° + 60°

sin ⁡ 3 π 8 = sin ⁡ 67.5 ∘ = 1 2 2 + 2 cos ⁡ 3 π 8 = cos ⁡ 67.5 ∘ = 1 2 2 − 2 tan ⁡ 3 π 8 = tan ⁡ 67.5 ∘ = 2 + 1 cot ⁡ 3 π 8 = cot ⁡ 67.5 ∘ = 2 − 1

72°: sum 36° + 36°

sin ⁡ 2 π 5 = sin ⁡ 72 ∘ = 1 4 2 ( 5 + 5 ) cos ⁡ 2 π 5 = cos ⁡ 72 ∘ = 1 4 ( 5 − 1 ) tan ⁡ 2 π 5 = tan ⁡ 72 ∘ = 5 + 2 5 cot ⁡ 2 π 5 = cot ⁡ 72 ∘ = 1 5 5 ( 5 − 2 5 )

75°: sum 30° + 45°

sin ⁡ 5 π 12 = sin ⁡ 75 ∘ = 1 4 ( 6 + 2 ) cos ⁡ 5 π 12 = cos ⁡ 75 ∘ = 1 4 ( 6 − 2 ) tan ⁡ 5 π 12 = tan ⁡ 75 ∘ = 2 + 3 cot ⁡ 5 π 12 = cot ⁡ 75 ∘ = 2 − 3

90°: fundamental

sin ⁡ π 2 = sin ⁡ 90 ∘ = 1 cos ⁡ π 2 = cos ⁡ 90 ∘ = 0 tan ⁡ π 2 = tan ⁡ 90 ∘  is undefined cot ⁡ π 2 = cot ⁡ 90 ∘ = 0

List of trigonometric constants to 2π/n

n sin ⁡ ( 2 π n ) cos ⁡ ( 2 π n ) tan ⁡ ( 2 π n ) 1 0 1 0 2 0 − 1 0 3 1 2 3 − 1 2 − 3 4 1 0 ± ∞ 5 1 4 ( 10 + 2 5 ) 1 4 ( 5 − 1 ) 5 + 2 5 6 1 2 3 1 2 3 7 1 2 1 3 ( 7 − ω 2 7 + 21 − 3 2 3 − ω 7 − 21 − 3 2 3 ) 1 6 ( − 1 + 7 + 21 − 3 2 3 + 7 − 21 − 3 2 3 ) 8 1 2 2 1 2 2 1 9 1 4 ( 4 ( − 1 + − 3 ) 3 + 4 ( − 1 − − 3 ) 3 ) 10 1 4 ( 10 − 2 5 ) 1 4 ( 5 + 1 ) 5 − 2 5 11 12 1 2 1 2 3 1 3 3 13 14 1 24 3 ( 112 − 14336 + − 5549064193 3 − 14336 − − 5549064193 3 ) 1 24 3 ( 80 + 14336 + − 5549064193 3 + 14336 − − 5549064193 3 ) 112 − 14336 + − 5549064193 3 − 14336 − − 5549064193 3 80 + 14336 + − 5549064193 3 + 14336 − − 5549064193 3 15 1 8 ( 15 + 3 − 10 − 2 5 ) 1 8 ( 1 + 5 + 30 − 6 5 ) 1 2 ( − 3 3 − 15 + 50 + 22 5 ) 16 1 2 ( 2 − 2 ) 1 2 ( 2 + 2 ) 2 − 1 17 1 16 ( − 1 + 17 + 34 − 2 17 + 2 17 + 3 17 − 34 − 2 17 − 2 34 + 2 17 ) 18 1 4 ( 4 − 1 − 4 3 3 − 4 − 1 + 4 3 3 ) 1 4 ( 4 + 4 − 3 3 + 4 − 4 − 3 3 ) 19 20 1 4 ( 5 − 1 ) 1 4 ( 10 + 2 5 ) 1 5 ( 25 − 10 5 ) 21 22 23 24 1 4 ( 6 − 2 ) 1 4 ( 6 + 2 ) 2 − 3

The trivial values

In degree format, sin and cos of 0, 30, 45, 60, and 90 can be calculated from their right angled triangles, using the Pythagorean theorem.

In radian format, sin and cos of π / 2ⁿ can be expressed in radical format by recursively applying the following:

2 cos ⁡ θ = 2 + 2 cos ⁡ 2 θ = 2 + 2 + 2 cos ⁡ 4 θ = 2 + 2 + 2 + 2 cos ⁡ 8 θ and so on. 2 sin ⁡ θ = 2 − 2 cos ⁡ 2 θ = 2 − 2 + 2 cos ⁡ 4 θ = 2 − 2 + 2 + 2 cos ⁡ 8 θ and so on.

For example:

cos ⁡ π 2 1 = 0 2 cos ⁡ π 2 2 = 2 + 0 2 and sin ⁡ π 2 2 = 2 − 0 2 cos ⁡ π 2 3 = 2 + 2 2 and sin ⁡ π 2 3 = 2 − 2 2 cos ⁡ π 2 4 = 2 + 2 + 2 2 and sin ⁡ π 2 4 = 2 − 2 + 2 2 cos ⁡ π 2 5 = 2 + 2 + 2 + 2 2 and sin ⁡ π 2 5 = 2 − 2 + 2 + 2 2 cos ⁡ π 2 6 = 2 + 2 + 2 + 2 + 2 2 and sin ⁡ π 2 6 = 2 − 2 + 2 + 2 + 2 2

and so on.

Radical form, sin and cos of π/(3 × 2n)

cos ⁡ π 3 × 2 0 = 1 2 cos ⁡ π 3 × 2 1 = 2 + 1 2 and sin ⁡ π 3 × 2 1 = 2 − 1 2 cos ⁡ π 3 × 2 2 = 2 + 3 2 and sin ⁡ π 3 × 2 2 = 2 − 3 2 cos ⁡ π 3 × 2 3 = 2 + 2 + 3 2 and sin ⁡ π 3 × 2 3 = 2 − 2 + 3 2 cos ⁡ π 3 × 2 4 = 2 + 2 + 2 + 3 2 and sin ⁡ π 3 × 2 4 = 2 − 2 + 2 + 3 2 cos ⁡ π 3 × 2 5 = 2 + 2 + 2 + 2 + 3 2 and sin ⁡ π 3 × 2 5 = 2 − 2 + 2 + 2 + 3 2

and so on.

Radical form, sin and cos of π/(5 × 2n)

cos ⁡ π 5 × 2 0 = 5 + 1 4 ( Therefore 2 + 2 cos ⁡ π 5 = 2 + 1.25 + 0.5 ) cos ⁡ π 5 × 2 1 = 2.5 + 1.25 2 and sin ⁡ π 5 × 2 1 = 1.5 − 1.25 2 cos ⁡ π 5 × 2 2 = 2 + 2.5 + 1.25 2 and sin ⁡ π 5 × 2 2 = 2 − 2.5 + 1.25 2 cos ⁡ π 5 × 2 3 = 2 + 2 + 2.5 + 1.25 2 and sin ⁡ π 5 × 2 3 = 2 − 2 + 2.5 + 1.25 2 cos ⁡ π 5 × 2 4 = 2 + 2 + 2 + 2.5 + 1.25 2 and sin ⁡ π 5 × 2 4 = 2 − 2 + 2 + 2.5 + 1.25 2 cos ⁡ π 5 × 2 5 = 2 + 2 + 2 + 2 + 2.5 + 1.25 2 and sin ⁡ π 5 × 2 5 = 2 − 2 + 2 + 2 + 2.5 + 1.25 2

and so on.

Radical form, sin and cos of π/(5 × 3 × 2n)

cos ⁡ π 15 × 2 1 = 0.703125 + 1.875 + 0.3125 + 1.75 2 cos ⁡ π 15 × 2 2 = 2 + 0.703125 + 1.875 + 0.3125 + 1.75 2 and sin ⁡ π 15 × 2 2 = 2 − 0.703125 + 1.875 + 0.3125 + 1.75 2 cos ⁡ π 15 × 2 3 = 2 + 2 + 0.703125 + 1.875 + 0.3125 + 1.75 2 and sin ⁡ π 15 × 2 3 = 2 − 2 + 0.703125 + 1.875 + 0.3125 + 1.75 2 cos ⁡ π 15 × 2 4 = 2 + 2 + 2 + 0.703125 + 1.875 + 0.3125 + 1.75 2 and sin ⁡ π 15 × 2 4 = 2 − 2 + 2 + 0.703125 + 1.875 + 0.3125 + 1.75 2 cos ⁡ π 15 × 2 5 = 2 + 2 + 2 + 2 + 0.703125 + 1.875 + 0.3125 + 1.75 2 and sin ⁡ π 15 × 2 5 = 2 − 2 + 2 + 2 + 0.703125 + 1.875 + 0.3125 + 1.75 2

and so on.

Radical form, sin and cos of π/(17 × 2n)

If M = 2 ( 17 + 17 ) and N = 2 ( 17 − 17 ) then

cos ⁡ π 17 = M − 4 + 2 ( N + 2 ( 2 M − N + 17 N − N − 8 M ) ) 8 .

Therefore, applying induction:

cos ⁡ π 17 × 2 0 = 30 + 2 17 + 136 − 8 17 + 272 + 48 17 + 8 34 − 2 17 × ( 17 − 1 ) − 64 34 + 2 17 8 ; cos ⁡ π 17 × 2 n + 1 = 2 + 2 cos ⁡ π 17 × 2 n 2 and sin ⁡ π 17 × 2 n + 1 = 2 − 2 c o s π 17 × 2 n 2 .

Radical form, sin and cos of π/(257 × 2n) and π/(65537 × 2n)

Note that the induction above can be applied in the same way to all the remaining Fermat primes (F₃=2²³+1=2⁸+1=257 and F₄=2²⁴+1=2¹⁶+1=65537), the factors of π whose cos and sin radical expressions are known to exist but are very long to express here.

cos ⁡ π 257 × 2 n + 1 = 2 + 2 cos ⁡ π 257 × 2 n 2 and sin ⁡ π 257 × 2 n + 1 = 2 − 2 cos ⁡ π 257 × 2 n 2 ; cos ⁡ π 65537 × 2 n + 1 = 2 + 2 cos ⁡ π 65537 × 2 n 2 and sin ⁡ π 65537 × 2 n + 1 = 2 − 2 cos ⁡ π 65537 × 2 n 2 .

Geometrical method

Applying Ptolemy's theorem to the cyclic quadrilateral ABCD defined by four successive vertices of the pentagon, we can find that:

crd ⁡ 36 ∘ = crd ⁡ ( ∠ A D B ) = a b = 2 1 + 5 = 5 − 1 2

which is the reciprocal 1/φ of the golden ratio. crd is the chord function,

crd ⁡   θ = 2 sin ⁡ θ 2 .

(See also Ptolemy's table of chords.)

Thus

sin ⁡ 18 ∘ = 1 1 + 5 = 5 − 1 4 .

(Alternatively, without using Ptolemy's theorem, label as X the intersection of AC and BD, and note by considering angles that triangle AXB is isosceles, so AX = AB = a. Triangles AXD and CXB are similar, because AD is parallel to BC. So XC = a·(a/b). But AX + XC = AC, so a + a²/b = b. Solving this gives a/b = 1/φ, as above).

Similarly

crd ⁡   108 ∘ = crd ⁡ ( ∠ A B C ) = b a = 1 + 5 2 ,

so

sin ⁡ 54 ∘ = cos ⁡ 36 ∘ = 1 + 5 4 .

Algebraic method

If θ is 18° or -54°, then 2θ and 3θ add up to 5θ = 90° or -270°, therefore sin 2θ is equal to cos 3θ.

( 2 sin ⁡ θ ) cos ⁡ θ = sin ⁡ 2 θ = cos ⁡ 3 θ = 4 cos 3 ⁡ θ − 3 cos ⁡ θ = ( 4 cos 2 ⁡ θ − 3 ) cos ⁡ θ = ( 1 − 4 sin 2 ⁡ θ ) cos ⁡ θ So, 4 sin 2 ⁡ θ + 2 sin ⁡ θ − 1 = 0 , which implies sin ⁡ θ = sin ⁡ ( 18 ∘ , − 54 ∘ ) = − 1 ± 5 4 .

Therefore,

sin ⁡ ( 18 ∘ ) = cos ⁡ ( 72 ∘ ) = 5 − 1 4 and sin ⁡ ( 54 ∘ ) = cos ⁡ ( 36 ∘ ) = 5 + 1 4 and sin ⁡ ( 36 ∘ ) = cos ⁡ ( 54 ∘ ) = 10 − 2 5 4 and sin ⁡ ( 72 ∘ ) = cos ⁡ ( 18 ∘ ) = 10 + 2 5 4 .

Alternately, the multiple-angle formulas for functions of 5x, where x ∈ {18, 36, 54, 72, 90} and 5x ∈ {90, 180, 270, 360, 450}, can be solved for the functions of x, since we know the function values of 5x. The multiple-angle formulas are:

sin ⁡ 5 x = 16 sin 5 ⁡ x − 20 sin 3 ⁡ x + 5 sin ⁡ x , cos ⁡ 5 x = 16 cos 5 ⁡ x − 20 cos 3 ⁡ x + 5 cos ⁡ x .

When sin 5x = 0 or cos 5x = 0, we let y = sin x or y = cos x and solve for y:

One solution is zero, and the resulting quartic equation can be solved as a quadratic in y².

When sin 5x = 1 or cos 5x = 1, we again let y = sin x or y = cos x and solve for y:

which factors into:

n × π/20

9° is 45 − 36, and 27° is 45 − 18; so we use the subtraction formulas for sine and cosine.

n × π/30

6° is 36 − 30, 12° is 30 − 18, 24° is 54 − 30, and 42° is 60 − 18; so we use the subtraction formulas for sine and cosine.

n × π/60

3° is 18 − 15, 21° is 36 − 15, 33° is 18 + 15, and 39° is 54 − 15, so we use the subtraction (or addition) formulas for sine and cosine.

Rationalizing the denominator

If the denominator is a square root, multiply the numerator and denominator by that radical. If the denominator is the sum or difference of two terms, multiply the numerator and denominator by the conjugate of the denominator. The conjugate is the identical, except the sign between the terms is changed. Sometimes you need to rationalize the denominator more than once.

Splitting a fraction in two

Sometimes it helps to split the fraction into the sum of two fractions and then simplify both separately.

Squaring and taking square roots

If there is a complicated term, with only one kind of radical in a term, this plan may help. Square the term, combine like terms, and take the square root. This may leave a big radical with a smaller radical inside, but it is often better than the original.

Simplifying nested radical expressions

In general nested radicals cannot be reduced. But if

a ± b c

with a, b, and c rational, we have

R = a 2 − b 2 c

is rational, then both

d = a + R 2  and  e = a − R 2

are rational; then we have

a ± b c = d ± e .

For example,

4 sin ⁡ 18 ∘ = 6 − 2 5 = 5 − 1. 4 sin ⁡ 15 ∘ = 2 2 − 3 = 2 ( 3 − 1 ) .