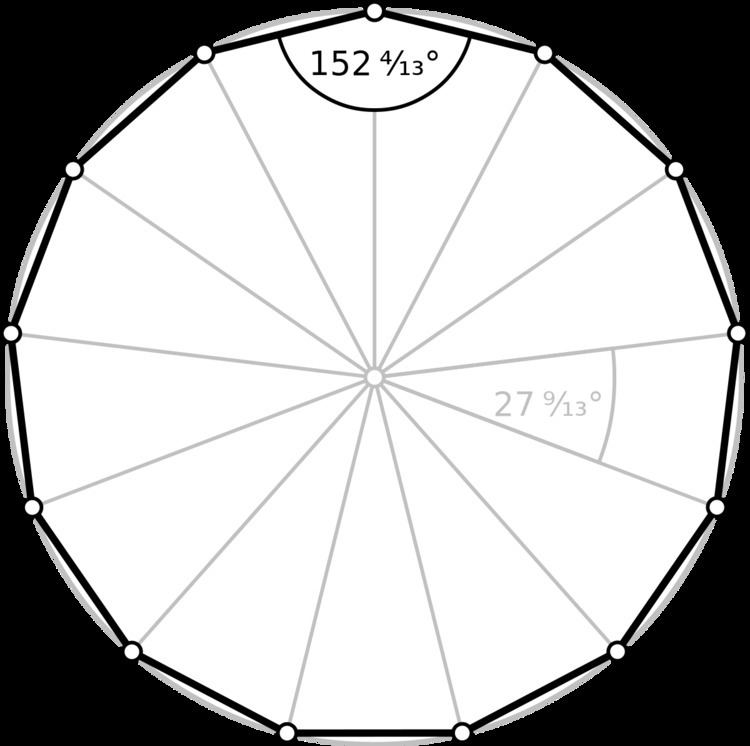
Schläfli symbol {13} Dual polygon Self | Edges and vertices 13 Internal angle (degrees) ≈152.308° | |
 | ||
Symmetry group Dihedral (D13), order 2×13 | ||
In geometry, a tridecagon or triskaidecagon or 13-gon is a thirteen-sided polygon.
Contents
Construction
As 13 is a Pierpont prime but not a Fermat prime, the regular tridecagon cannot be constructed using a compass and straightedge. However, it is constructible using neusis, or an angle trisector.
The following is an animation from a neusis construction of a regular tridecagon with radius of circumcircle
An approximate construction of a regular tridecagon using straightedge and compass is shown here.
Another possible animation of an approximate construction, also possible with using straightedge and compass.
GeoGebra:
GeoGebra: 360° ÷ 13 = 27.69230769230769°
Absolute error of
Example to illustrate the error:
At a circumscribed circle radius r = 1 billion km (the light needed for this distance about 55 minutes), the absolute error of the 1st side would be approximately 1.5 mm.
For details, see: Wikibooks: Tridecagon, construction description (German)
Symmetry
The regular tridecagon has Dih13 symmetry, order 26. Since 13 is a prime number there is one subgroup with dihedral symmetry: Dih1, and 2 cyclic group symmetries: Z13, and Z1.
These 4 symmetries can be seen in 4 distinct symmetries on the tridecagon. John Conway labels these by a letter and group order. Full symmetry of the regular form is r26 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g13 subgroup has no degrees of freedom but can seen as directed edges.
Numismatic use
The regular tridecagon is used as the shape of the Czech 20 korun coin.
Related polygons
A tridecagram is a 13-sided star polygon. There are 5 regular forms given by Schläfli symbols: {13/2}, {13/3}, {13/4}, {13/5}, and {13/6}.
Petrie polygons
The regular tridecagon is the Petrie polygon 12-simplex:
