Traced monoidal category - Alchetron, the free social encyclopedia

In category theory, a traced monoidal category is a category with some extra structure which gives a reasonable notion of feedback.

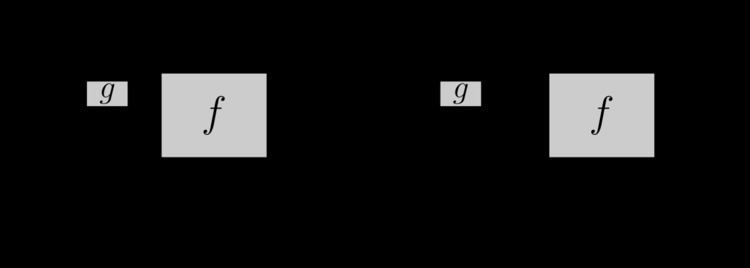
A traced symmetric monoidal category is a symmetric monoidal category C together with a family of functions

T r X , Y U : C ( X ⊗ U , Y ⊗ U ) → C ( X , Y )

called a trace, satisfying the following conditions (where we sometimes denote an identity morphism by the corresponding object, e.g., using U to denote id U ):

naturality in X: for every f : X ⊗ U → Y ⊗ U and g : X ′ → X ,

naturality in Y: for every f : X ⊗ U → Y ⊗ U and g : Y → Y ′ ,

dinaturality in U: for every f : X ⊗ U → Y ⊗ U ′ and g : U ′ → U

vanishing I: for every f : X ⊗ I → Y ⊗ I ,

vanishing II: for every f : X ⊗ U ⊗ V → Y ⊗ U ⊗ V

superposing: for every f : X ⊗ U → Y ⊗ U and g : W → Z ,

yanking:

(where γ is the symmetry of the monoidal category).

Properties

Every compact closed category admits a trace.

Given a traced monoidal category C, the Int construction generates the free (in some bicategorical sense) compact closure Int(C) of C.

References

Traced monoidal category Wikipedia

(Text) CC BY-SA