Thomson problem

Mathematical statement

The physical system embodied by the Thomson problem is a special case of one of eighteen unsolved mathematics problems proposed by the mathematician Steve Smale — "Distribution of points on the 2-sphere". The solution of each N-electron problem is obtained when the N-electron configuration constrained to the surface of a sphere of unit radius, r = 1 , yields a global electrostatic potential energy minimum, U ( N ) .

The electrostatic interaction energy occurring between each pair of electrons of equal charges ( e i = e j = e , with e the elementary charge of an electron) is given by Coulomb's Law,

Here, k e is Coulomb's constant and r i j = | r i − r j | is the distance between each pair of electrons located at points on the sphere defined by vectors r i and r j , respectively.

Simplified units of e = 1 and k e = 1 are used without loss of generality. Then,

The total electrostatic potential energy of each N-electron configuration may then be expressed as the sum of all pair-wise interactions

The global minimization of U ( N ) over all possible collections of N distinct points is typically found by numerical minimization algorithms.

Example

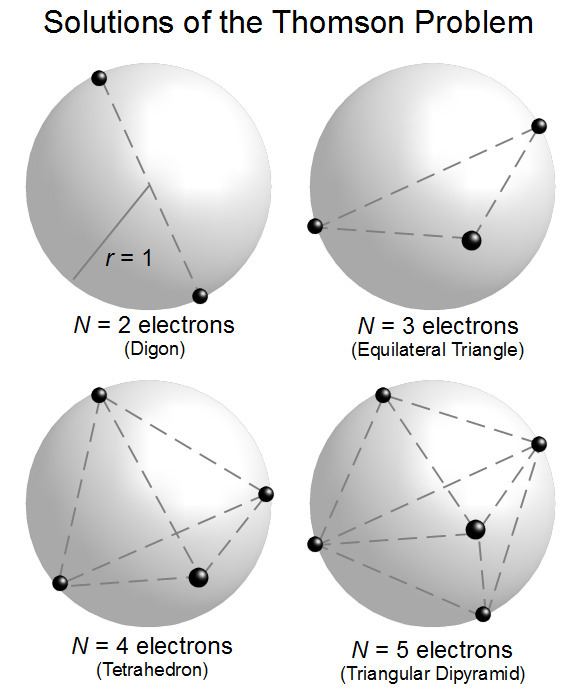
The solution of the Thomson problem for two electrons is obtained when both electrons are as far apart as possible on opposite sides of the origin, r i j = 2 r = 2 , or

Known solutions

Minimum energy configurations have been rigorously identified in only a handful of cases.

Notably, the geometric solutions of the Thomson problem for N = 4, 6, and 12 electrons are known as Platonic solids whose faces are all congruent equilateral triangles. Numerical solutions for N=8 and 20 are not the regular convex polyhedral configurations of the remaining two Platonic solids, whose faces are square and pentagonal, respectively.

Generalizations

One can also ask for ground states of particles interacting with arbitrary potentials. To be mathematically precise, let f be a decreasing real-valued function, and define the energy functional ∑ i < j f ( | x i − x j | )

Traditionally, one considers f ( x ) = x − α . Notable cases include α = ∞, the Tammes problem (packing); α = 1, the Thomson problem; α = 0, Whyte's problem (to maximize the product of distances).

One may also consider configurations of N points on a sphere of higher dimension. See spherical design.

Relations to other scientific problems

The Thomson problem is a natural consequence of Thomson's plum pudding model in the absence of its uniform positive background charge.

Though experimental evidence led to the abandonment of Thomson's plum pudding model as a complete atomic model, irregularities observed in numerical energy solutions of the Thomson problem have been found to correspond with electron shell-filling in naturally occurring atoms throughout the periodic table of elements.

The Thomson problem also plays a role in the study of other physical models including multi-electron bubbles and the surface ordering of liquid metal drops confined in Paul traps.

The generalized Thomson problem arises, for example, in determining the arrangements of the protein subunits which comprise the shells of spherical viruses. The "particles" in this application are clusters of protein subunits arranged on a shell. Other realizations include regular arrangements of colloid particles in colloidosomes, proposed for encapsulation of active ingredients such as drugs, nutrients or living cells, fullerene patterns of carbon atoms, and VSEPR Theory. An example with long-range logarithmic interactions is provided by the Abrikosov vortices which would form at low temperatures in a superconducting metal shell with a large monopole at the center.

Configurations of smallest known energy

In the following table N is the number of points (charges) in a configuration, E 1 is the energy, the symmetry type is given in Schönflies notation (see Point groups in three dimensions), and r i are the positions of the charges. Most symmetry types require the vector sum of the positions (and thus the electric dipole moment) to be zero.

It is customary to also consider the polyhedron formed by the convex hull of the points. Thus, v i is the number of vertices where the given number of edges meet, ' e is the total number of edges, f 3 is the number of triangular faces, f 4 is the number of quadrilateral faces, and θ 1 is the smallest angle subtended by vectors associated with the nearest charge pair. Note that the edge lengths are generally not equal; thus (except in the cases N = 4, 6, 12, 24) the convex hull is only topologically equivalent to the uniform polyhedron or Johnson solid listed in the last column.

According to a conjecture, if m = n + 2 , p is the polyhedron formed by the convex hull of m points, q is the number of quadrilateral faces of p, then the solution for m electrons is f(m): f ( m ) = 0 n + 3 ∗ n − q .