 | ||
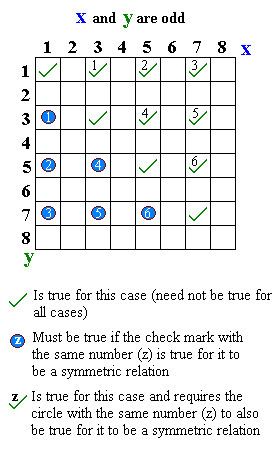
In mathematics and other areas, a binary relation R over a set X is symmetric if it holds for all a and b in X that a is related to b if and only if b is related to a.
Contents
- In mathematics
- Outside mathematics
- Relationship to asymmetric and antisymmetric relations
- Additional aspects
- References
In mathematical notation, this is:
In mathematics
Outside mathematics
Relationship to asymmetric and antisymmetric relations
By definition, a relation cannot be both symmetric and asymmetric (where if a is related to b, then b cannot be related to a (in the same way)). However, a relation can be neither symmetric nor asymmetric, which is the case for "is less than or equal to" and "preys on").
Symmetric and antisymmetric (where the only way a can be related to b and b be related to a is if a = b) are actually independent of each other, as these examples show.
Additional aspects
A symmetric relation that is also transitive and reflexive is an equivalence relation.
One way to conceptualize a symmetric relation in graph theory is that a symmetric relation is an edge, with the edge's two vertices being the two entities so related. Thus, symmetric relations and undirected graphs are combinatorially equivalent objects.
