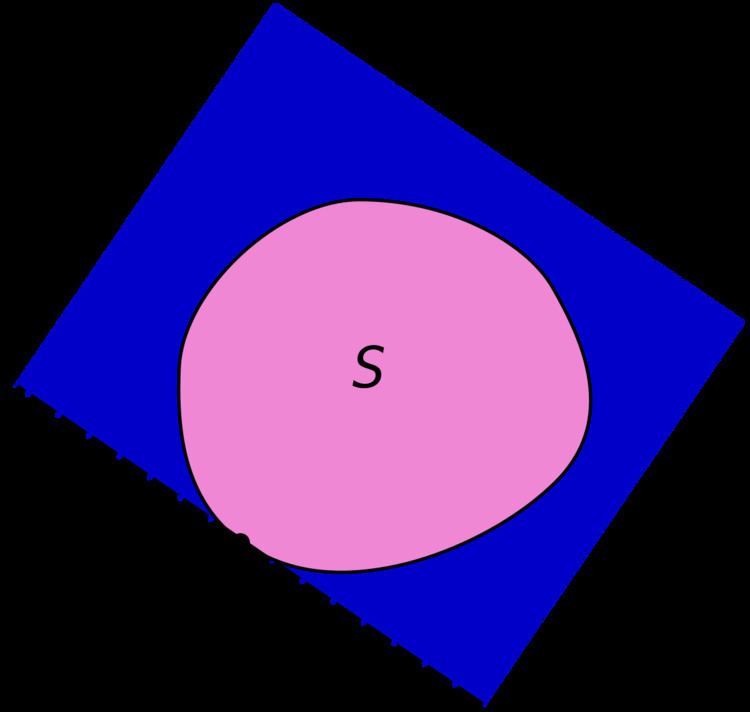
In geometry, a supporting hyperplane of a set S in Euclidean space R n is a hyperplane that has both of the following two properties:
S is entirely contained in one of the two closed half-spaces bounded by the hyperplane S has at least one boundary-point on the hyperplane.Here, a closed half-space is the half-space that includes the points within the hyperplane.
This theorem states that if S is a convex set in the topological vector space X = R n , and x 0 is a point on the boundary of S , then there exists a supporting hyperplane containing x 0 . If x ∗ ∈ X ∗ ∖ { 0 } ( X ∗ is the dual space of X , x ∗ is a nonzero linear functional) such that x ∗ ( x 0 ) ≥ x ∗ ( x ) for all x ∈ S , then
H = { x ∈ X : x ∗ ( x ) = x ∗ ( x 0 ) } defines a supporting hyperplane.
Conversely, if S is a closed set with nonempty interior such that every point on the boundary has a supporting hyperplane, then S is a convex set.
The hyperplane in the theorem may not be unique, as noticed in the second picture on the right. If the closed set S is not convex, the statement of the theorem is not true at all points on the boundary of S , as illustrated in the third picture on the right.
The supporting hyperplanes of convex sets are also called tac-planes or tac-hyperplanes.
A related result is the separating hyperplane theorem, that every two disjoint convex sets can be separated by a hyperplane.