Supriya Ghosh (Editor)

Superparabola

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Superparabola

The superparabola is a geometric curve defined in the Cartesian coordinate system as a set of points (x, y) with

Contents

y / b = [ 1 − ( x / a ) 2 ] p

where p, a, and b are positive integers. The equation defines an open curve in the rectangle − a ≤ x ≤ a, 0 ≤ y ≤ b.

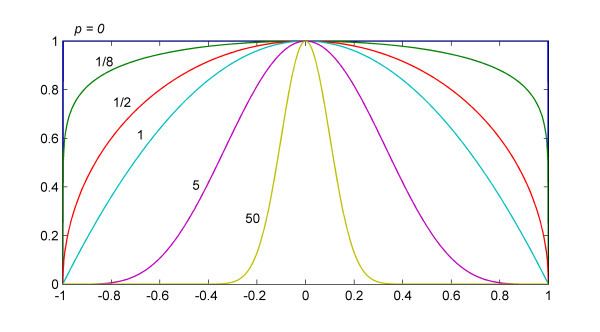
The superparabola can vary in shape from a rectangular function (p = 0) , to a semi-ellipse ( p = 1/2 ), to a parabola (p = 1), to a pulse function (p > 1) .

Mathematical properties

Without loss of generality we can consider the canonical form of the superparabola( a = b = 1)

f ( x ; p ) = ( 1 − x 2 ) p

When p > 0 the function describes a continuous differentiable curve on the plane. The curve can be described parametrically on the complex plane as

z = sin (u) +i cos 2p(u);     − π/2 ≤ u ≤ π/2

Derivatives of the superparabola are given by

f ′ ( x ; p ) = − 2 p x ( 1 − x 2 ) p − 1
∂ f ∂ p = ( 1 − x 2 ) p ln ( 1 − x 2 ) = f ( x ) ln [ f ( x ; 1 ) ]

The area under the curve is given by

Area = ∫ − 1 1 ∫ 0 f ( x ) d y d x = ∫ − 1 1 ( 1 − x 2 ) p d x = ψ ( p )

where ψ is a global function valid for all p > − 1 ,

ψ ( p ) = π Γ ( p + 1 ) Γ ( p + 3 / 2 )

The area under a portion of the curve requires the indefinite integral

∫ ( 1 − x 2 ) p d x = x 2 F 1 ( 1 / 2 , − p ; 3 / 2 ; x 2 )

where 2 F 1 is the Gauss hypergeometric function. An interesting property is that any superparabola raised to a power n is just another superparabola, thus

∫ − 1 1 f n ( x ) = ψ ( n p )

The centroid of the area under the curve is given by

C = i A ∫ − 1 1 x ∫ 0 f ( x ) d y d x + j A   ∫ − 1 1 ∫ 0 f ( x ) y d y d x
= j 2 A ∫ − 1 1 f 2 ( x ) d x = j ψ ( 2 p ) 2 ψ ( p )

where the x -component is zero by virtue of symmetry. Thus, the centroid can be expressed as one-half the ratio of the area of the square of the curve to the area of the curve.

The nth (mathematical) moment is given by

μ = ∫ − 1 1 x n f ( x ) d x = { M ( p , n ) if n is even 0 if n is odd
M ( p , n ) = 2 n + 1 Γ ( ( n + 3 ) / 2 ) Γ ( p + 1 ) Γ ( p + ( n + 3 ) / 2 )

The arc length of the curve is given by

Length = ∫ − 1 1 1 + [ f ′ ( x ) ] 2 d x

In general, integrals containing 1 + [ f ′ ( x ) ] 2 cannot be found in terms of standard mathematical functions. Even numerical solutions can be problematic for the improper integrals that arise when f ′ ( x ) is singular at x = ± 1 . Two instances of exact solutions have been found. For the semicircle ( p = 1 / 2 ) , L = π and the parabola ( p = 1 ) , L = ( 5 + sinh − 1 ⁡ ( 2 ) / 2 ) ≈ 2.9579 .

The arc length is L = 4 for both p = 0  and  p = ∞ and has a minimum value of L ∼ 2.914 at p ∼ 1.595 . The area under the curve decreases monotonically with increasing p .

Generalization

A natural generalization for the superparabola is to relax the constraint on the power of x. For example,

f ( x ) = ( 1 − | x | q ) p

where the absolute value was added to assure symmetry with respect to the y-axis. The curve can be described parametrically on the complex plane as well,

z = | sin 2 / q ( u ) | sgn ( u ) + i cos 2 p ( u ) ;            − π / 2 ≤ u ≤ π / 2

Now, it is apparent that the generalized superparabola contains within it the superellipse, i.e., p = 1 / q , and its generalization. Conversely, the generalization of the superellipse clearly contains the superparabola. Here, however, we have the analytic solution for the area under the curve.

The indefinite and definite integrals are given by

∫ f ( x ) d x = x ⋅ 2 F 1 ( − p , 1 / q ; 1 + 1 / q ; x 2 )
Area = ∫ − 1 1 f ( x ) d x = Ψ ( p , q )

where Ψ is a universal function valid for all q and p > − 1 .

Ψ ( p , q ) = 2 Γ ( q + 1 q ) Γ ( p + 1 ) Γ ( p + q + 1 q )

These results can be readily applied to the centroid and moments of the curve as demonstrated above by substitution of Ψ ( p , q ) for ψ ( p ) .

History

The superellipse has been identified since 1818 as a Lamé curve. It appears that the superparabola was first identified by Löffelmann and Gröller. in their paper on superquadrics in conjunction with computer graphics. Waldman and Gray used the superparabola in their analyses of the Archimedean hoof. The "cylinder hoof", "hoof" or "ungula" was first formulated in a letter from Archimedes to Eratosthenes in the 3rd century BC and led to the classic Propositions 13 and 14 of The Method. This letter now transposed in Dijksterhuis is one of the most famous exchange of ideas in all history of mathematics.

Applications

The superparabola and its generalization have been applied to the Archimedean hoof. Briefly, the Archimedean hoof consists of a right cylinder with a footprint y = f(x) and height h that is cut by the plane z = h y . In the first image, the portion on the right is called the hoof, and is taken from the remaining half-cylinder leaving the complement . The base area, volume, and center of mass of both the hoof and the complement can be described solely in terms of the universal function, Ψ and height.

References

Superparabola Wikipedia
(Text) CC BY-SA