Trisha Shetty (Editor)

Superformula

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Superformula httpsuploadwikimediaorgwikipediacommonsthu

Processing tutorial creating trippy animations with the superformula


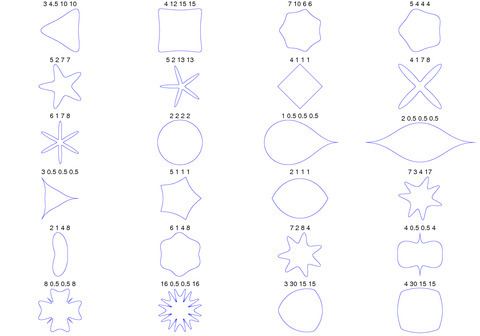
The superformula is a generalization of the superellipse and was proposed by Johan Gielis around 2000. Gielis suggested that the formula can be used to describe many complex shapes and curves that are found in nature. Gielis holds a patent related to the synthesis of patterns generated by the superformula.

Contents

In polar coordinates, with r the radius and φ the angle, the superformula is:

r ( φ ) = ( | cos ⁡ ( m 1 φ 4 ) a | n 2 + | sin ⁡ ( m 2 φ 4 ) b | n 3 ) − 1 n 1 .

By choosing different values for the parameters a , b , m 1 , m 2 , n 1 , n 2 , and n 3 , different shapes can be generated.

The formula was obtained by generalizing the superellipse, named and popularized by Piet Hein, a Danish mathematician.

Extension to higher dimensions

It is possible to extend the formula to 3, 4, or n dimensions, by means of the spherical product of superformulas. For example, the 3D parametric surface is obtained by multiplying two superformulas r1 and r2. The coordinates are defined by the relations:

x = r 1 ( θ ) cos ⁡ θ ⋅ r 2 ( ϕ ) cos ⁡ ϕ , y = r 1 ( θ ) sin ⁡ θ ⋅ r 2 ( ϕ ) cos ⁡ ϕ , z = r 2 ( ϕ ) sin ⁡ ϕ ,

where ϕ (latitude) varies between −π/2 and π/2 and θ (longitude) between −π and π.

Generalization

The superformula can be generalized by replacing the parameter m 1 with y and m 2 with z:

r ( φ ) = ( | cos ⁡ ( y φ 4 ) a | n 2 + | sin ⁡ ( z φ 4 ) b | n 3 ) − 1 n 1

This allows the creation of rotationally asymmetric and nested structures. In the following examples a, b, n 2 and n 3 are 1:

A GNU Octave program for generating these figures:

3D superformula: a = b = 1; m 1 = m 2 = m, n1, n2 and n3 are shown in the pictures.

A GNU Octave program for generating these figures:

References

Superformula Wikipedia
(Text) CC BY-SA


Similar Topics