String topology

Motivation

While the singular cohomology of a space has always a product structure, this is not true for the singular homology of a space. Nevertheless, it is possible to construct such a structure for an oriented manifold M of dimension d. This is the so-called intersection product. Intuitively, one can describe it as follows: given classes x ∈ H p ( M ) and y ∈ H q ( M ) , take their product x × y ∈ H p + q ( M × M ) and make it transversal to the diagonal M ↪ M × M . The intersection is then a class in H p + q − d ( M ) , the intersection product of x and y. One way to make this construction rigorous is to use stratifolds.

Another case, where the homology of a space has a product, is the (based) loop space Ω X of a space X. Here the space itself has a product

by going first the first loop and then the second. There is no analogous product structure for the free loop space LX of all maps from S 1 to X since the two loops need not have a common point. A substitute for the map m is the map

where Map(8, M) is the subspace of L M × L M , where the value of the two loops coincides at 0 and γ is defined again by composing the loops. (Here "8" denotes the topological space "figure 8", i.e. the wedge of two circles.)

The Chas–Sullivan product

The idea of the Chas–Sullivan product is to now combine the product structures above. Consider two classes x ∈ H p ( L M ) and y ∈ H q ( L M ) . Their product x × y lies in H p + q ( L M × L M ) . We need a map

One way to construct this is to use stratifolds (or another geometric definition of homology) to do transversal intersection (after interpreting M a p ( 8 , M ) ⊂ L M × L M as an inclusion of Hilbert manifolds). Another approach starts with the collapse map from LM x LM to the Thom space of the normal bundle of Map(8, M). Composing the induced map in homology with the Thom isomorphism, we get the map we want.

Now we can compose i^! with the induced map of γ to get a class in H p + q − d ( L M ) , the Chas–Sullivan product of x and y (see e.g. Cohen & Jones 2002).

Remarks

The Batalin–Vilkovisky structure

There is an action S 1 × L M → L M by rotation, which induces a map

Plugging in the fundamental class [ S 1 ] ∈ H 1 ( S 1 ) , gives an operator

of degree 1. One can show that this operator interacts nicely with the Chas–Sullivan product in the sense that they form together the structure of a Batalin–Vilkovisky algebra on H ∗ ( L M ) . This operator tends to be difficult to compute in general.

Field theories

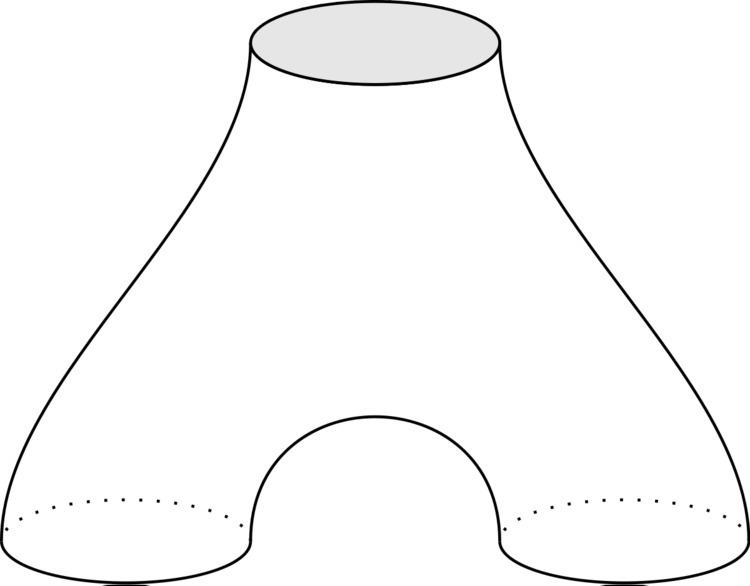
There are several attempts to construct (topological) field theories via string topology. The basic idea is to fix an oriented manifold M and associate to every surface with p incoming and q outgoing boundary components (with n ≥ 1 ) an operation

which fulfills the usual axioms for a topological field theory. The Chas–Sullivan product is associated to the pair of pants. It can be shown that these operations are 0 if the genus of the surface is greater than 0 (see Tamanoi2010)

A more structured approach (exhibited in Godin2008) gives ( H ∗ ( L M ) , H ∗ ( L M ) ) the structure of a degree d open-closed homological conformal field theory (HCFT) with positive boundary. Ignoring the open-closed part, this amounts to the following structure: let S be a surface with boundary, where the boundary circles are labeled as incoming or outcoming. If there are p incoming and q outgoing and n ≥ 1 , we get operations

parametrized by a certain twisted homology of the mapping class group of S.