Neha Patil (Editor)

String diagram

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
String diagram

In category theory, string diagrams are a way of representing 2-cells in 2-categories.

Contents

Definition

The idea is to represent structures of dimension d by structures of dimension 2-d, using the Poincaré duality. Thus,

  • an object is represented by a portion of plane,
  • a 1-cell f : A → B is represented by a vertical segment — called a string — separating the plane in two (the left part corresponding to A and the right one to B),
  • a 2-cell α : f ⇒ g : A → B is represented by an intersection of strings (the strings corresponding to f above the link, the strings corresponding to g below the link).

    • The parallel composition of 2-cells corresponds to the horizontal juxtaposition of diagrams and the sequential composition to the vertical juxtaposition of diagrams.

    Example

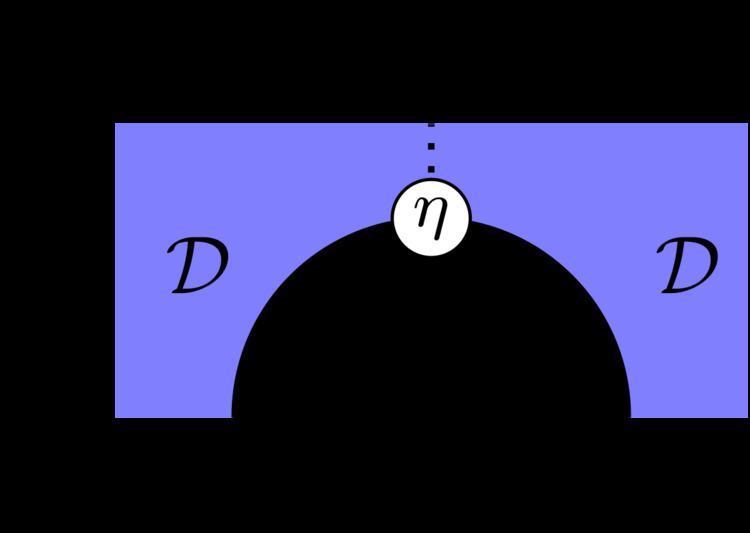
    Consider an adjunction ( F , G , η , ε ) between two categories C and D where F : C ← D is left adjoint of G : C → D and the natural transformations η : I → G F and ε : F G → I are respectively the unit and the counit. The string diagrams corresponding to these natural transformations are:

    The string corresponding to the identity functor is drawn as a dotted line and can be omitted. The definition of an adjunction requires the following equalities:

    ( ε F ) ∘ F ( η ) = 1 F G ( ε ) ∘ ( η G ) = 1 G

    The first one is depicted as

    Other diagrammatic languages

    Monoidal categories can also be pictured this way since a strict monoidal category can be seen as a 2-category with only one object (there will therefore be only one type of plane) and Mac Lane's strictness theorem states that any monoidal category is monoidally equivalent to a strict one. The graphical language of string diagrams for monoidal categories may be extended to represent expressions in categories with other structure, such as symmetric monoidal categories, dagger categories, and is related to geometric presentations for braided monoidal categories and ribbon categories.

    References

    String diagram Wikipedia
    (Text) CC BY-SA