Stirling numbers of the first kind

Definitions

The original definition of Stirling numbers of the first kind was algebraic. These numbers, usually written s(n, k), are signed integers whose sign, positive or negative, depends on the parity of n − k. Afterwards, the absolute values of these numbers, |s(n, k)|, which are known as unsigned Stirling numbers of the first kind, were found to count permutations, so in combinatorics the (signed) Stirling numbers of the first kind, s(n, k), are often defined as counting numbers multiplied by a sign factor. That is the approach taken on this page.

Most identities on this page are stated for unsigned Stirling numbers. Note that the notations on this page are not universal.

Unsigned Stirling numbers of the first kind

The unsigned Stirling numbers of the first kind are denoted in various ways by different authors. Common notations are c ( n , k ) , | s ( n , k ) | and [ n k ] . (The last is also common notation for the Gaussian coefficients.) They count the number of permutations of n elements with k disjoint cycles. For example, of the 3 ! = 6 permutations of three elements, there is one permutation with three cycles (the identity permutation, given in one-line notation by 123 or in cycle notation by ( 1 ) ( 2 ) ( 3 ) ), three permutations with two cycles ( 132 = ( 1 ) ( 23 ) , 213 = ( 3 ) ( 12 ) , and 321 = ( 2 ) ( 13 ) ) and two permutations with one cycle ( 312 = ( 132 ) and 231 = ( 123 ) ). Thus, [ 3 3 ] = 1 , [ 3 2 ] = 3 and [ 3 1 ] = 2 .

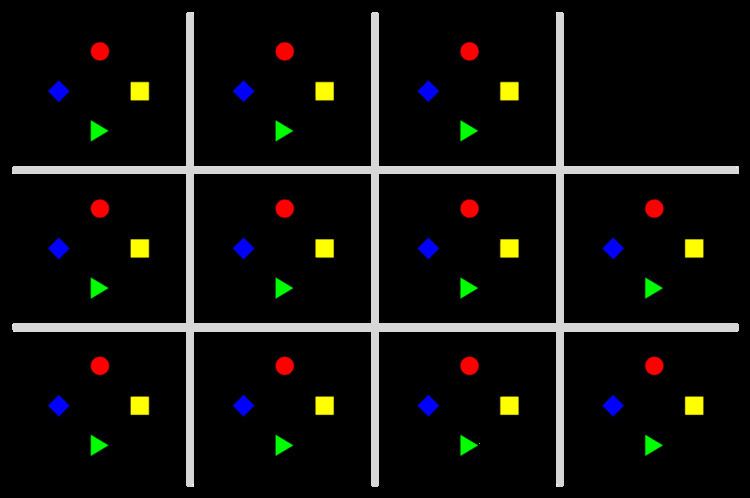
As a second example, the image at right shows that [ 4 2 ] = 11 : the symmetric group on 4 objects has 3 permutations of the form

( ∙ ∙ ) ( ∙ ∙ ) —2 orbits, each of size 2,

and 8 permutations of the form

( ∙ ∙ ∙ ) ( ∙ ) —1 orbit of size 3 and 1 orbit of size 1.

The unsigned Stirling numbers also arise as coefficients of the rising factorial, i.e.,

( x ) ( n ) = x ( x + 1 ) ⋯ ( x + n − 1 ) = ∑ k = 0 n [ n k ] x k .

Thus, for example, ( x ) ( 3 ) = x ( x + 1 ) ( x + 2 ) = 1 ⋅ x 3 + 3 ⋅ x 2 + 2 ⋅ x , which matches the computations in the preceding paragraph.

Stirling numbers of the first kind

Stirling numbers of the first kind (sometimes with the qualifying adjective signed) are given by

s ( n , k ) = ( − 1 ) n − k [ n k ] .

They are the coefficients in the expansion

( x ) n = ∑ k = 0 n s ( n , k ) x k ,

where ( x ) n is the falling factorial

( x ) n = x ( x − 1 ) ( x − 2 ) ⋯ ( x − n + 1 ) .

Note that

[ n k ] = | s ( n , k ) | .

Recurrence relation

The unsigned Stirling numbers of the first kind can be calculated by the recurrence relation

[ n + 1 k ] = n [ n k ] + [ n k − 1 ]

for k > 0 , with the initial conditions

[ 0 0 ] = 1 and [ n 0 ] = [ 0 n ] = 0

for n > 0.

It follows immediately that the (signed) Stirling numbers of the first kind satisfy the recurrence

s ( n + 1 , k ) = − n s ( n , k ) + s ( n , k − 1 ) .

Algebraic proof

We prove the recurrence relation using the definition of Stirling numbers in terms of rising factorials. Distributing the last term of the product, we have

( x ) ( n + 1 ) = x ( x + 1 ) ⋯ ( x + n − 1 ) ( x + n ) = n ( x ) ( n ) + x ( x ) ( n ) .

The coefficient of x^k on the left-hand side of this equation is [ n + 1 k ] . The coefficient of x^k in n(x)⁽ⁿ⁾ is n ⋅ [ n k ] , while the coefficient of x^k in x (x)⁽ⁿ⁾ is [ n k − 1 ] . Since the two sides are equal as polynomials, the coefficients of x^k on both sides must be equal, and the result follows.

Combinatorial proof

We prove the recurrence relation using the definition of Stirling numbers in terms of permutations with a given number of cycles (or equivalently, orbits).

Consider forming a permutation of n + 1 objects from a permutation of n objects by adding a distinguished object. There are exactly two ways in which this can be accomplished. We could do this by forming a singleton cycle, i.e., leaving the extra object alone. This increases the number of cycles by 1 and so accounts for the [ n k − 1 ] term in the recurrence formula. We could also insert the new object into one of the existing cycles. Consider an arbitrary permutation of n objects with k cycles, and label the objects a₁, ..., a_n, so that the permutation is represented by

( a 1 … a j 1 ) ( a j 1 + 1 … a j 2 ) … ( a j k − 1 + 1 … a n ) ⏟ k   c y c l e s .

To form a new permutation of n + 1 objects and k cycles one must insert the new object into this array. There are n ways to perform this insertion, inserting the new object immediately following any of the n already present. This explains the n [ n k ] term of the recurrence relation. These two cases include all possibilities, so the recurrence relation follows.

Table of values for small n and k

Below is a triangular array of unsigned values for the Stirling numbers of the first kind, similar in form to Pascal's triangle. These values are easy to generate using the recurrence relation in the previous section.

Simple identities

Note that although

[ 0 0 ] = 1 , we have [ n 0 ] = 0 if n > 0

and

[ 0 k ] = 0 if k > 0, or more generally [ n k ] = 0 if k > n.

Also

[ n 1 ] = ( n − 1 ) ! , [ n n ] = 1 , [ n n − 1 ] = ( n 2 ) ,

and

[ n n − 2 ] = 1 4 ( 3 n − 1 ) ( n 3 )  and  [ n n − 3 ] = ( n 2 ) ( n 4 ) .

Similar relationships involving the Stirling numbers hold for the Bernoulli polynomials. Many relations for the Stirling numbers shadow similar relations on the binomial coefficients. The study of these 'shadow relationships' is termed umbral calculus and culminates in the theory of Sheffer sequences.

Combinatorial proofs

These identities may be derived by enumerating permutations directly. For example, a permutation of n elements with n − 3 cycles must have one of the following forms:

n − 6 fixed points and three two-cycles

n − 5 fixed points, a three-cycle and a two-cycle, or

n − 4 fixed points and a four-cycle.

The three types may be enumerated as follows:

choose the six elements that go into the two-cycles, decompose them into two-cycles and take into account that the order of the cycles is not important:

choose the five elements that go into the three-cycle and the two-cycle, choose the elements of the three-cycle and take into account that three elements generate two three-cycles:

choose the four elements of the four-cycle and take into account that four elements generate six four-cycles:

Sum the three contributions to obtain

( n 6 ) ( 6 2 , 2 , 2 ) 1 6 + ( n 5 ) ( 5 3 ) × 2 + ( n 4 ) × 6 = ( n 2 ) ( n 4 ) .

Other relations

Other relations involving Stirling numbers of the first kind include

[ n 2 ] = ( n − 1 ) ! H n − 1 ,

where H_n is a harmonic number, and

[ n 3 ] = 1 2 ( n − 1 ) ! [ ( H n − 1 ) 2 − H n − 1 ( 2 ) ] [ n 4 ] = 1 3 ! ( n − 1 ) ! [ ( H n − 1 ) 3 − 3 H n − 1 H n − 1 ( 2 ) + 2 H n − 1 ( 3 ) ]

where H_n^(m) is a generalized harmonic number. For a generalization of this relation, see below.

For all positive integer m and n we have that

( n + m ) ! = ∑ k = 0 n ∑ j = 0 m m n − k ¯ [ m j ] ( n k ) k ! ,

where a b ¯ = a ( a + 1 ) ⋯ ( a + b − 1 ) is the Pochhammer symbol. This formula is a dual of Spivey's result for the Bell numbers.

Generating function

A variety of identities may be derived by manipulating the generating function:

H ( z , u ) = ( 1 + z ) u = ∑ n = 0 ∞ ( u n ) z n = ∑ n = 0 ∞ z n n ! ∑ k = 0 n s ( n , k ) u k = ∑ k = 0 ∞ u k ∑ n = k ∞ z n n ! s ( n , k ) .

Using the equality

( 1 + z ) u = e u log ⁡ ( 1 + z ) = ∑ k = 0 ∞ ( log ⁡ ( 1 + z ) ) k u k k ! ,

it follows that

∑ n = k ∞ ( − 1 ) n − k [ n k ] z n n ! = ( log ⁡ ( 1 + z ) ) k k ! .

(This identity is valid for formal power series, and the sum converges in the complex plane for |z| < 1.) Other identities arise by exchanging the order of summation, taking derivatives, making substitutions for z or u, etc. For example, we may derive:

( 1 − z ) − u = ∑ k = 0 ∞ u k ∑ n = k ∞ z n n ! [ n k ] = e u log ⁡ ( 1 / ( 1 − z ) )

and

∑ n = i ∞ [ n i ] n ( n ! ) = ζ ( i + 1 )

where ζ ( k ) is the Riemann zeta function.

Finite sums

Since permutations are partitioned by number of cycles, one has

∑ k = 0 n [ n k ] = n !

The identity

∑ p = k n [ n p ] ( p k ) = [ n + 1 k + 1 ]

can be proved by the techniques on the page Stirling numbers and exponential generating functions.

Explicit formula

The Stirling number s(n,n-p) can be found from the formula

s ( n , n − p ) = 1 ( n − p − 1 ) ! ∑ 0 ≤ k 1 , … , k p : ∑ 2 p m k m = p ( − 1 ) K ( n + K − 1 ) ! k 2 ! ⋯ k p !   1 ! k 1 2 ! k 2 3 ! k 3 ⋯ p ! k p ,

where K = k 2 + ⋯ + k p . The sum is a sum over all partitions of p.