Star product

Definition

The star product of two graded posets ( P , ≤ P ) and ( Q , ≤ Q ) , where P has a unique maximal element 1 ^ and Q has a unique minimal element 0 ^ , is a poset P ∗ Q on the set ( P ∖ { 1 ^ } ) ∪ ( Q ∖ { 0 ^ } ) . We define the partial order ≤ P ∗ Q by x ≤ y if and only if:

In other words, we pluck out the top of P and the bottom of Q , and require that everything in P be smaller than everything in Q .

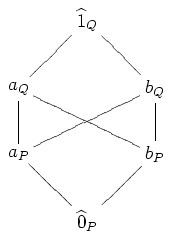
Example

For example, suppose P and Q are the Boolean algebra on two elements.

Then P ∗ Q is the poset with the Hasse diagram below.

Properties

The star product of Eulerian posets is Eulerian.