Samiksha Jaiswal (Editor)

Spline wavelet

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Spline wavelet

In the mathematical theory of wavelets, a spline wavelet is a wavelet constructed using a spline function. There are different types of spline wavelets. The interpolatory spline wavelets introduced by C.K. Chui and J.Z. Wang are based on a certain spline interpolation formula. Though these wavelets are orthogonal, they do not have compact supports. There is a certain class of wavelets, unique in some sense, constructed using B-splines and having compact supports. Even though these wavelets are not orthogonal they have some special properties that have made them quite popular. The terminology spline wavelet is sometimes used to refer to the wavelets in this class of spline wavelets. These special wavelets are also called B-spline wavelets and cardinal B-spline wavelets. The Battle-Lemarie wavelets are also wavelets constructed using spline functions.

Contents

Cardinal B-splines

Let n be a fixed non-negative integer. Let Cn denote the set of all real-valued functions defined over the set of real numbers such that each function in the set as well its first n derivatives are continuous everywhere. A bi-infinite sequence . . . x−2, x−1, x0, x1, x2, . . . such that xr < xr+1 for all r and such that xr approaches ±∞ as r approaches ±∞ is said to define a set of knots. A spline of order n with a set of knots {xr} is a function S(x) in Cn such that, for each r, the restriction of S(x) to the interval [xr, xr+1) coincides with a polynomial with real coefficients of degree at most n in x.

If the separation xr+1 - xr, where r is any integer, between the successive knots in the set of knots is a constant, the spline is called a cardinal spline. The set of integers Z = {. . ., -2, -1, 0, 1, 2, . . .} is a standard choice for the set of knots of a cardinal spline. Unless otherwise specified, it is generally assumed that the set of knots is the set of integers.

A cardinal B-spline is a special type of cardinal spline. For any positive integer m the cardinal B-spline of order m, denoted by Nm'(x), is defined recursively as follows.

N 1 ( x ) = { 1 0 ≤ x < 1 0 otherwise N m ( x ) = ∫ 0 1 N m − 1 ( x − t ) d t , for m > 1 .

Concrete expressions for the cardinal B-splines of all orders up to 5 and their graphs are given later in this article.

Elementary properties

  1. The support of N m ( x ) is the closed interval [ 0 , m ] .
  2. The function N m ( x ) is non-negative, that is, N m ( x ) > 0 for 0 < x < m .
  3. ∑ k = − ∞ ∞ N m ( x − k ) = 1 for all x .
  4. The cardinal B-splines of orders m and m-1 are related by the identity: N m ( x ) = x m − 1 N m − 1 ( x ) + m − x m − 1 N m − 1 ( x − 1 ) .
  5. The function N m ( x ) is symmetrical about x = m 2 , that is, N m ( m 2 − x ) = N m ( m 2 + x ) .
  6. The derivative of N m ( x ) is given by N m ′ ( x ) = N m − 1 ( x ) − N m − 1 ( x − 1 ) .
  7. ∫ − ∞ ∞ N m ( x ) d x = 1

Two-scale relation

The cardinal B-spline of order m satisfies the following two-scale relation:

N m ( x ) = ∑ k = 0 m 2 − m + 1 ( m k ) N m ( 2 x − k ) .

Riesz property

The cardinal B-spline of order m satisfies the following property, known as the Riesz property: There exists two positive real numbers A and B such that for any square summable two-sided sequence { c k } k = − ∞ ∞ and for any x,

A ∥ { c k } ∥ 2 ≤ ∥ ∑ k = − ∞ ∞ c k N m ( x − k ) ∥ 2 ≤ B ∥ { c k } ∥ 2

where ∥ ⋅ ∥ is the norm in the ℓ2-space.

Cardinal B-splines of small orders

The cardinal B-splines are defined recursively starting from the B-spline of order 1, namely N 1 ( x ) , which takes the value 1 in the interval [0, 1) and 0 elsewhere. Computer algebra systems may have to be employed to obtain concrete expressions for higher order cardinal B-splines. The concrete expressions for cardinal B-splines of all orders up to 6 are given below. The graphs of cardinal B-splines of orders up to 4 are also exhibited. In the images, the graphs of the terms contributing to the corresponding two-scale relations are also shown. The two dots in each image indicate the extremities of the interval supporting the B-spline.

Constant B-spline

The B-spline of order 1, namely N 1 ( x ) , is the constant B-spline. It is defined by

N 1 ( x ) = { 1 0 ≤ x < 1 0 otherwise

The two-scale relation for this B-spline is

N 1 ( x ) = N 1 ( 2 x ) + N 1 ( 2 x − 1 )

Linear B-spline

The B-spline of order 2, namely N 2 ( x ) , is the linear B-spline. It is given by

N 2 ( x ) = { x 0 ≤ x < 1 − x + 2 1 ≤ x < 2 0 otherwise

The two-scale relation for this wavelet is

N 2 ( x ) = 1 2 N 2 ( 2 x ) + N 2 ( 2 x − 1 ) + 1 2 N 2 ( 2 x − 2 )

Quadratic B-spline

The B-spline of order 3, namely N 3 ( x ) , is the quadratic B-spline. It is given by

N 3 ( x ) = { 1 2 x 2 0 ≤ x < 1 − x 2 + 3 x − 3 2 1 ≤ x < 2 1 2 x 2 − 3 x + 9 2 2 ≤ x < 3 0 otherwise

The two-scale relation for this wavelet is

N 3 ( x ) = 1 4 N 3 ( 2 x ) + 3 4 N 3 ( 2 x − 1 ) + 3 4 N 3 ( 2 x − 2 ) + 1 4 N 3 ( 2 x − 3 )

Cubic B-spline

The cubic B-spline is the cardinal B-spline of order 4, denoted by N 4 ( x ) . It is given by the following expressions:

N 4 ( x ) = { 1 6 x 3 0 ≤ x < 1 − 1 2 x 3 + 2 x 2 − 2 x + 2 3 1 ≤ x < 2 1 2 x 3 − 4 x 2 + 10 x − 22 3 2 ≤ x < 3 − 1 6 x 3 + 2 x 2 − 8 x + 32 3 3 ≤ x < 4 0 otherwise

The two-scale relation for the cubic B-spline is

N 4 ( x ) = 1 8 N 4 ( 2 x ) + 1 2 N 4 ( 2 x − 1 ) + 3 4 N 4 ( 2 x − 2 ) + 1 2 N 4 ( 2 x − 3 ) + 1 8 N 4 ( 2 x − 4 )

Bi-quadratic B-spline

The bi-quadratic B-spline is the cardinal B-spline of order 5 denoted by N 5 ( x ) . It is given by

N 5 ( x ) = { 1 24 x 4 0 ≤ x < 1 − 1 6 x 4 + 5 6 x 3 − 5 4 x 2 + 5 6 x − 5 24 1 ≤ x < 2 1 4 x 4 − 5 2 x 3 + 35 4 x 2 − 25 2 x + 155 24 2 ≤ x < 3 − 1 6 x 4 + 5 2 x 3 − 55 4 x 2 + 65 2 x − 655 24 3 ≤ x < 4 1 24 x 4 − 5 6 x 3 + 25 4 x 2 − 125 6 x + 625 24 4 ≤ x < 5 0 otherwise

The two-scale relation is

N 5 ( x ) = 1 16 N 5 ( 2 x ) + 5 16 N 5 ( 2 x − 1 ) + 10 16 N 5 ( 2 x − 2 ) + 10 16 N 5 ( 2 x − 3 ) + 5 16 N 5 ( 2 x − 4 ) + 1 16 N 5 ( 2 x − 5 )

Quintic B-spline

The quintic B-spline is the cardinal B-spline of order 6 denoted by N 6 ( x ) . It is given by

N 6 ( x ) = { 1 120 x 5 0 ≤ x < 1 − 1 24 x 5 + 1 4 x 4 − 1 2 x 3 + 1 2 x 2 − 1 4 x + 1 20 1 ≤ x < 2 1 12 x 5 − x 4 + 9 2 x 3 − 19 2 x 2 + 39 4 x − 79 20 2 ≤ x < 3 − 1 12 x 5 + 3 2 x 4 − 21 2 x 3 + 71 2 x 2 − 231 4 x + 731 20 3 ≤ x < 4 1 24 x 5 − x 4 + 19 2 x 3 − 89 2 x 2 + 409 4 x − 1829 20 4 ≤ x < 5 − 1 120 x 5 + 1 4 x 4 − 3 x 3 + 18 x 2 − 54 x + 324 5 5 ≤ x < 6 0 otherwise

Multi-resolution analysis generated by cardinal B-splines

The cardinal B-spline N m ( x ) of order m generates a multi-resolution analysis. In fact, from the elementary properties of these functions enunciated above, it follows that the function N m ( x ) is square integrable and is an element of the space L 2 ( R ) of square integrable functions. To set up the multi-resolution analysis the following notations used.

  • For any integers k , j , define the function N m , k j ( x ) = N m ( 2 k x − j ) .
  • For each integer k , define the subspace V k of L 2 ( R ) as the closure of the linear span of the set { N m , k j ( x ) : j = ⋯ , − 2 , − 1 , 0 , 1 , 2 , ⋯ } .

    • That these define a multi-resolution analysis follows from the following:

    1. The spaces V k satisfy the property: ⋯ ⊂ V − 2 ⊂ V − 1 ⊂ V 0 ⊂ V 1 ⊂ V 2 ⊂ ⋯ .
    2. The closure in L 2 ( R ) of the union of all the subspaces V k is the whole space L 2 ( R ) .
    3. The intersection of all the subspaces V k is the singleton set containing only the zero function.
    4. For each integer k the set { N m , k j ( x ) : j = ⋯ , − 2 , − 1 , 0 , 1 , 2 , ⋯ } is an unconditional basis for V k . (A sequence {xn} in a Banach space X is an unconditional basis for the space X if every permutation of the sequence {xn} is also a basis for the same space X.)

    Wavelets from cardinal B-splines

    Let m be a fixed positive integer and N m ( x ) be the cardinal B-spline of order m. A function ψ m ( x ) in L 2 ( R ) is a basic wavelet relative to the cardinal B-spline function N m ( x ) if the closure in L 2 ( R ) of the linear span of the set { ψ m ( x − j ) : j = ⋯ , − 2 , − 1 , 0 , 1 , 2 , ⋯ } (this closure is denoted by W 0 ) is the orthogonal complement of V 0 in V 1 . The subscript m in ψ m ( x ) is used to indicate that ψ m ( x ) is a basic wavelet relative the cardinal B-spline of order m. There is no unique basic wavelet ψ m ( x ) relative to the cardinal B-spline N m ( x ) . Some of these are discussed in the following sections.

    Definitions

    Let m be a fixed positive integer and let N m ( x ) be the cardinal B-spline of order m. Given a sequence { f j : j = ⋯ , − 2 , − 1 , 0 , 1 , 2 , ⋯ } of real numbers, the problem of finding a sequence { c m , k : k = ⋯ , − 2 , − 1 , 0 , 1 , 2 , ⋯ } of real numbers such that

    ∑ k = − ∞ ∞ c m , k N m ( j + m 2 − k ) = f j for all j ,

    is known as the cardinal spline interpolation problem. The special case of this problem where the sequence { f j } is the sequence δ 0 j , where δ i j is the Kronecker delta function δ i j defined by

    δ i j = { 1 ,  if  i = j 0 ,  if  i ≠ j ,

    is the fundamental cardinal spline interpolation problem. The solution of the problem yields the fundamental cardinal interpolatory spline of order m. This spline is denoted by L m ( x ) and is given by

    L m ( x ) = ∑ k = − ∞ ∞ c m , k N m ( x + m 2 − k )

    where the sequence { c m , k } is now the solution of the following system of equations:

    ∑ k = − ∞ ∞ c m , k N m ( j + m 2 − k ) = δ 0 j

    Procedure to find the fundamental cardinal interpolatory spline

    The fundamental cardinal interpolatory spline L m ( x ) can be determined using Z-transforms. Using the following notations

    A ( z ) = ∑ k = − ∞ ∞ δ k 0 z k = 1 , B m ( z ) = ∑ k = − ∞ ∞ N m ( k + m 2 ) z k , C m ( z ) = ∑ k = − ∞ ∞ c m , k z k ,

    it can be seen from the equations defining the sequence c m , k that

    B m ( z ) C m ( z ) = A ( z )

    from which we get

    C m ( z ) = 1 B m ( z ) .

    This can be used to obtain concrete expressions for c m , k .

    Example

    As a concrete example, the case L 4 ( x ) may be investigated. The definition of B m ( z ) implies that

    B 4 ( x ) = ∑ k = − ∞ ∞ N 4 ( 2 + k ) z k

    The only nonzero values of N 4 ( k + 2 ) are given by k = − 1 , 0 , 1 and the corresponding values are

    N 4 ( 1 ) = 1 6 , N 4 ( 2 ) = 4 6 , N 4 ( 3 ) = 1 6 .

    Thus B 4 ( z ) reduces to

    B 4 ( z ) = 1 6 z − 1 + 4 6 z 0 + 1 6 z 1 = 1 + 4 z + z 2 6 z

    This yields the following expression for C 4 ( z ) .

    C 4 ( z ) = 6 z 1 + 4 z + z 2

    Splitting this expression into partial fractions and expanding each term in powers of z in an annular region the values of c 4 , k can be computed. These values are then substituted in the expression for L 4 ( x ) to yield

    L 4 ( x ) = ∑ k = − ∞ ∞ ( − 1 ) k 3 ( 2 − 3 ) | k | N 4 ( x + 2 − k )

    Wavelet using fundamental interpolatory spline

    For a positive integer m, the function ψ m ( x ) defined by

    ψ I , m ( x ) = d m d x m L 2 m ( 2 x − 1 )

    is a basic wavelet relative to the cardinal B-spline of order N m ( x ) . The subscript I in ψ I , m is used to indicate that it is based in the interpolatory spline formula. This basic wavelet is not compactly supported.

    Example

    The wavelet of order 2 using interpolatory spline is given by

    ψ I , 2 ( x ) = d 2 d x 2 L 4 ( 2 x − 1 )

    The expression for L 4 ( x ) now yields the following formula:

    ψ I , 2 ( x ) = d 2 d x 2 ∑ k = − ∞ ∞ ( − 1 ) k 3 ( 2 − 3 ) | k | N 4 ( 2 x + 1 − k )

    Now, using the expression for the derivative of N m ( x ) in terms of N m − 1 ( x ) the function ψ 2 ( x ) can be put in the following form:

    ψ I , 2 ( x ) = ∑ k = − ∞ ∞ ( − 1 ) k 4 3 ( 2 − 3 ) | k | ( ( N 2 ( 2 x + k − 1 ) − 2 N 2 ( 2 x + k − 2 ) + N 2 ( 2 x + k − 3 ) )

    The following piecewise linear function is the approximation to ψ 2 ( x ) obtained by taking the sum of the terms corresponding to k = − 3 , … , 3 in the infinite series expression for ψ 2 ( x ) .

    ψ I , 2 ( x ) ≈ { 0.07142668 x + 0.17856670 − 2.5 < x ≤ − 2 − 0.48084803 x − 0.92598272 − 2 < x ≤ − 1.5 2.0088293 x + 2.8085333 − 1.5 < x ≤ − 1 − 7.5684795 x − 6.7687755 − 1 < x ≤ − 0.5 28.245949 x + 11.138439 − 0.5 < x ≤ 0 − 57.415316 x + 11.138439 0 < x ≤ 0.5 57.415316 x − 46.276878 0.5 < x ≤ 1 − 28.245949 x + 39.384388 1 < x ≤ 1.5 7.5684795 x − 14.337255 1.5 < x ≤ 2 − 2.0088293 x + 4.8173625 2 < x ≤ 2.5 0.48084803 x − 1.4068308 2.5 < x ≤ 3 − 0.07142668 x + 0.24999338 3 < x ≤ 3.5 0 o t h e r w i s e

    Two-scale relation

    The two-scale relation for the wavelet function ψ m ( x ) is given by

    ψ I , m ( x ) = ∑ − ∞ ∞ q n N m ( 2 x − n ) where q n = ∑ j = 0 m ( − 1 ) j ( m j ) c m + n − j − 1 .

    Compactly supported B-spline wavelets

    The spline wavelets generated using the interpolatory wavelets are not compactly supported. Compactly supported B-spline wavelets were discovered by Charles K. Chui and Jian-zhong Wang and published in 1991. The compactly supported B-spline wavelet relative to the cardinal B-spline N m ( x ) of order m discovered by Chui and Wong and denoted by ψ C , m ( x ) , has as its support the interval [ 0 , 2 m − 1 ] . These wavelets are essentially unique in a certain sense explained below.

    Definition

    The compactly supported B-spline wavelet of order m is given by

    ψ C , m ( x ) = 1 2 2 m − 1 ∑ j = 0 2 m − 2 ( − 1 ) j N 2 m ( j + 1 ) d m d x m N 2 m ( 2 x − j )

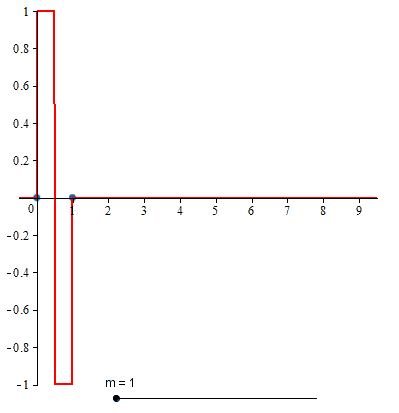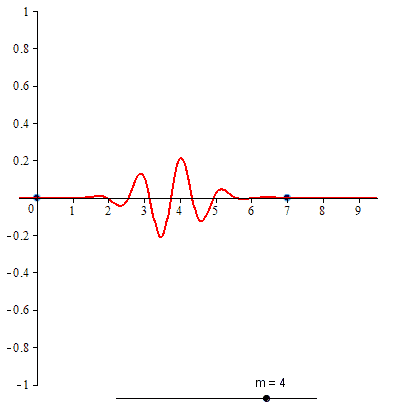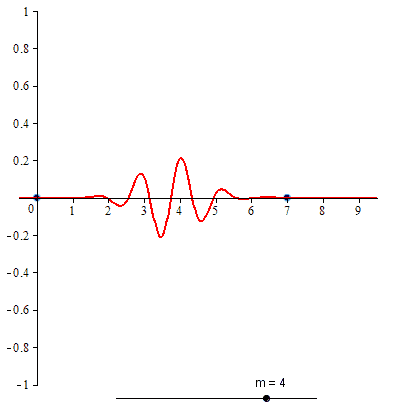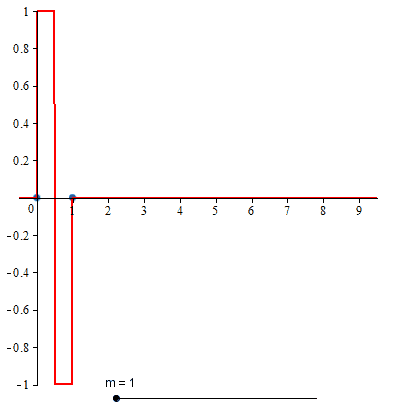
    This is an m-th order spline. As a special case, the compactly supported B-spline wavelet of order 1 is

    ψ C , 1 ( x ) = 1 2 N 2 ( 1 ) d d x N 2 ( 2 x ) = { 1 0 ≤ x < 1 2 − 1 1 2 ≤ x < 1 0 otherwise

    which is the well-known Haar wavelet.

    Properties

    1. The support of ψ C , m ( x ) is the closed interval [ 0 , 2 m − 1 ] .
    2. The wavelet ψ C , m ( x ) is the unique wavelet with minimum support in the following sense: If η ( x ) ∈ W 0 generates W 0 and has support not exceeding 2 m − 1 in length then η ( x ) = c 0 ψ C , m ( x − n 0 ) for some nonzero constant c 0 and for some integer n 0 .
    3. ψ C , m ( x ) is symmetric for even m and antisymmetric for odd m.

    Two-scale relation

    ψ m ( x ) satisfies the two-scale relation:

    ψ C , m ( x ) = ∑ n = 0 3 m − 2 q n N m ( 2 x − n ) where q n = ( − 1 ) n 2 m − 1 ∑ j = 0 m ( m j ) N 2 m ( n − j + 1 ) .

    Decomposition relation

    The decomposition relation for the compactly supported B-spline wavelet has the following form:

    N m ( 2 x − l ) = ∑ k = − ∞ ∞ [ a m , l − 2 k N m ( x − k ) + b m , l − 2 k ψ C , m ( x − k ) ]

    where the coefficients a m , j and b m , j are given by

    a m , j = − ( − 1 ) j 2 ∑ l = − ∞ ∞ q − j + 2 m − 2 l + 1 c 2 m , l , b m , j = ( − 1 ) j 2 ∑ l = − ∞ ∞ p − j + 2 m − 2 l + 1 c 2 m , l .

    Here the sequence c 2 m , l is the sequence of coefficients in the fundamental interpolatoty cardinal spline wavelet of order m.

    Compactly supported B-spline wavelet of order 1

    The two-scale relation for the compactly supported B-spline wavelet of order 1 is

    ψ C , 1 ( x ) = N 1 ( 2 x ) − N 1 ( 2 x − 1 )

    The closed form expression for compactly supported B-spline wavelet of order 1 is

    ψ C , 1 ( x ) = { 1 0 ≤ x < 1 2 − 1 1 2 ≤ x < 1 0 otherwise

    Compactly supported B-spline wavelet of order 2

    The two-scale relation for the compactly supported B-spline wavelet of order 2 is

    ψ C , 2 ( x ) = 1 12 ( N 2 ( 2 x ) − 6 N 2 ( 2 x − 1 ) + 10 N 2 ( 2 x − 2 ) − 6 N 2 ( 2 x − 3 ) + N 2 ( 2 x − 4 ) )

    The closed form expression for compactly supported B-spline wavelet of order 2 is

    ψ C , 2 ( x ) = { 1 6 x 0 ≤ x < 1 2 − 7 6 x + 2 3 1 2 ≤ x < 1 8 3 x − 19 6 1 ≤ x < 3 2 − 8 3 x + 29 6 3 2 ≤ x < 2 7 6 x − 17 6 2 ≤ x < 5 2 − 1 6 x + 1 2 5 2 ≤ x < 3 0 otherwise

    Compactly supported B-spline wavelet of order 3

    The two-scale relation for the compactly supported B-spline wavelet of order 3 is

    ψ C , 3 ( x ) = 1 480 [ ( N 3 ( 2 x ) − 29 N 3 ( 2 x − 1 ) + 147 N 3 ( 2 x − 2 ) − 303 N 3 ( 2 x − 3 ) +

    The closed form expression for compactly supported B-spline wavelet of order 3 is

    ψ C , 3 ( x ) = { 1 240 x 2 0 ≤ x < 1 2 − 31 240 x 2 + 2 15 x − 1 30 1 2 ≤ x < 1 103 120 x 2 − 221 120 x + 229 240 1 ≤ x < 3 2 − 313 120 x 2 + 1027 120 x − 1643 240 3 2 ≤ x < 2 22 5 x 2 − 779 40 x + 339 16 2 ≤ x < 5 2 − 22 5 x 2 + 981 40 x − 541 16 5 2 ≤ x < 3 313 120 x 2 − 701 40 x + 2341 80 3 ≤ x < 7 2 − 103 120 x 2 + 809 120 x − 3169 240 7 2 ≤ x < 4 31 240 x 2 − 139 120 x + 623 240 4 ≤ x < 9 2 − 1 240 x 2 + 1 24 x − 5 48 9 2 ≤ x < 5 0 otherwise

    Compactly supported B-spline wavelet of order 4

    The two-scale relation for the compactly supported B-spline wavelet of order 4 is

    ψ C , 4 ( x ) = 1 40320 [ N 4 ( 2 x ) − 124 N 4 ( 2 x − 1 ) + 1677 N 4 ( 2 x − 2 ) − 7904 N 4 ( 2 x − 3 ) + 18482 N 4 ( 2 x − 4 ) −

    The closed form expression for compactly supported B-spline wavelet of order 4 is

    ψ C , 4 ( x ) = { 1 30240 x 3 0 ≤ x < 1 2 − 127 30240 x 3 + 2 315 x 2 − 1 315 x + 1 1890 1 2 ≤ x < 1 19 280 x 3 − 47 224 x 2 + 2147 10080 x − 103 1440 1 ≤ x < 3 2 − 1109 2520 x 3 + 465 224 x 2 − 32413 10080 x + 16559 10080 3 2 ≤ x < 2 5261 3360 x 3 − 33463 3360 x 2 + 42043 2016 x − 145193 10080 2 ≤ x < 5 2 − 35033 10080 x 3 + 93577 3360 x 2 − 148517 2016 x + 216269 3360 5 2 ≤ x < 3 4832 945 x 3 − 27691 560 x 2 + 113923 720 x − 28145 168 3 ≤ x < 7 2 − 4832 945 x 3 + 58393 1008 x 2 − 52223 240 x + 2048227 7560 7 2 ≤ x < 4 35033 10080 x 3 − 75827 1680 x 2 + 981101 5040 x − 234149 840 4 ≤ x < 9 2 − 5261 3360 x 3 + 38509 1680 x 2 − 112487 1008 x + 30347 168 9 2 ≤ x < 5 1109 2520 x 3 − 24077 3360 x 2 + 78311 2016 x − 141311 2016 5 ≤ x < 11 2 − 19 280 x 3 + 1361 1120 x 2 − 14617 2016 x + 4151 288 11 2 ≤ x < 6 127 30240 x 3 − 55 672 x 2 + 5359 10080 x − 11603 10080 6 ≤ x < 13 2 − 1 30240 x 3 + 1 1440 x 2 − 7 1440 x + 49 4320 13 2 ≤ x < 7 0 otherwise

    Compactly supported B-spline wavelet of order 5

    The two-scale relation for the compactly supported B-spline wavelet of order 5 is

    ψ C , 5 ( x ) = 1 5806080 [ N 5 ( 2 x ) − 507 N 5 ( 2 x − 1 ) + 17128 N 5 ( 2 x − 2 ) − 166304 N 5 ( 2 x − 3 ) + 748465 N 5 ( 2 x − 4 )

    The closed form expression for compactly supported B-spline wavelet of order 5 is

    ψ C , 5 ( x ) = { 1 8709120 x 4 0 ≤ x < 1 2 − 73 1244160 x 4 + 1 8505 x 3 − 1 11340 x 2 + 1 34020 x − 1 272160 1 2 ≤ x < 1 9581 4354560 x 4 − 19417 2177280 x 3 + 1303 96768 x 2 − 19609 2177280 x + 6547 2903040 1 ≤ x < 3 2 − 118931 4354560 x 4 + 366119 2177280 x 3 − 186253 483840 x 2 + 121121 311040 x − 427181 2903040 3 2 ≤ x < 2 759239 4354560 x 4 − 3146561 2177280 x 3 + 6466601 1451520 x 2 − 13202873 2177280 x + 26819897 8709120 2 ≤ x < 5 2 − 2980409 4354560 x 4 + 5183893 725760 x 3 − 13426333 483840 x 2 + 426589 8960 x − 12635243 414720 5 2 ≤ x < 3 7873577 4354560 x 4 − 16524079 725760 x 3 + 7385369 69120 x 2 − 17868671 80640 x + 497668543 290304 3 ≤ x < 7 2 − 14714327 4354560 x 4 + 108543091 2177280 x 3 − 56901557 207360 x 2 + 1454458651 2177280 x − 5286189059 8709120 7 2 ≤ x < 4 15619 3402 x 4 − 33822017 435456 x 3 + 15828929 32256 x 2 − 597598433 435456 x + 277413649 193536 4 ≤ x < 9 2 − 15619 3402 x 4 + 38150335 435456 x 3 − 20157247 32256 x 2 + 859841695 435456 x − 64472345 27648 9 2 ≤ x < 5 14714327 4354560 x 4 − 4466137 62208 x 3 + 165651247 290304 x 2 − 875490655 435456 x + 4614904015 1741824 5 ≤ x < 11 2 − 7873577 4354560 x 4 + 30717383 725760 x 3 − 179437319 483840 x 2 + 16606729 11520 x − 869722273 414720 11 2 ≤ x < 6 2980409 4354560 x 4 − 12698561 725760 x 3 + 16211669 96768 x 2 − 19138891 26880 x + 3289787993 2903040 6 ≤ x < 13 2 − 759239 4354560 x 4 + 10519741 2177280 x 3 − 10403603 207360 x 2 + 71964499 311040 x − 3481646837 8709120 13 2 ≤ x < 7 118931 4354560 x 4 − 1774639 2177280 x 3 + 630259 69120 x 2 − 14096161 311040 x + 245108501 2903040 7 ≤ x < 15 2 − 9581 4354560 x 4 + 21863 311040 x 3 − 407387 483840 x 2 + 9758873 2177280 x − 25971499 2903040 15 2 ≤ x < 8 73 1244160 x 4 − 4343 2177280 x 3 + 5273 207360 x 2 − 313703 2177280 x + 380873 1244160 8 ≤ x < 17 2 − 1 8709120 x 4 + 1 241920 x 3 − 1 17920 x 2 + 3 8960 x − 27 35840 17 2 ≤ x < 9 0 otherwise

    Battle-Lemarie wavelets

    The Battle-Lemarie wavelets form a class of orthonormal wavelets constructed using the class of cardinal B-splines. The expressions for these wavelets are given in the frequency domain; that is, they are defined by specifying their Fourier transforms. The Fourier transform of a function of t, say, F ( t ) , is denoted by F ^ ( ω ) .

    Definition

    Let m be a positive integer and let N m ( x ) be the cardinal B-spline of order m. The Fourier transform of N m ( x ) is N ^ m ( ω ) . The scaling function ϕ m ( t ) for the m-th order Battle-Lemarie wavelet is that function whose Fourier transform is

    ϕ ^ m ( ω ) = N ^ m ( ω ) ( ∑ k = − ∞ ∞ | N ^ m ( ω + 2 π k ) | 2 ) 1 / 2 .

    The m-th order Battle-Lemarie wavelet is the function ψ B L , m ( t ) whose Fourier transform is

    ψ ^ B L , m ( ω ) = − e − i ω / 2 ϕ ^ m ( ω + 2 π ) ¯ ϕ ^ m ( ω 2 ) ϕ ^ m ( ω 2 + π ) ¯

    Additional reading

  • Amir Z Averbuch and Valery A Zheludev (2007). "Wavelet transforms generated by splines" (PDF). Int. J. Wavelets Multiresolut Inf. Process. 257 (5). Retrieved 21 December 2014. 
  • Amir Z. Averbuch, Pekka Neittaanmaki, and Valery A. Zheludev (2014). Spline and Spline Wavelet Methods with Applications to Signal and Image Processing Volume I. Springer. ISBN 978-94-017-8925-7.  CS1 maint: Multiple names: authors list (link)

    • References

    Spline wavelet Wikipedia
    (Text) CC BY-SA