Sphere–cylinder intersection - Alchetron, the free social encyclopedia

In the theory of analytic geometry for real three-dimensional space, the intersection between a sphere and a cylinder can be a circle, a point, the empty set, or a special type of curve.

Sphere lies entirely within cylinder

If a + R < r , the sphere lies entirely in the interior of the cylinder. The intersection is the empty set.

Sphere touches cylinder in one point

If the sphere is smaller than the cylinder ( R < r ) and a + R = r , the sphere lies in the interior of the cylinder except for one point. The intersection is the single point ( r , 0 , 0 ) .

Sphere centered on cylinder axis

If the center of the sphere lies on the axis of the cylinder, a = 0 . In that case, the intersection consists of two circles of radius r . These circles lie in the planes

z = ± R 2 − r 2 ;

If r = R , the intersection is a single circle in the plane z = 0 .

Non-trivial cases

Subtracting the two equations given above gives

z 2 + ( r 2 − R 2 + a 2 ) = 2 a x .

Since x is a quadratic function of z , the projection of the intersection onto the xz-plane is the section of an orthogonal parabola; it is only a section due to the fact that − r < x < r . The vertex of the parabola lies at point ( − b , 0 , 0 ) , where

b = R 2 − r 2 − a 2 2 a .

Intersection consists of two closed curves

If R > r + a , the condition x < r cuts the parabola into two segments. In this case, the intersection of sphere and cylinder consists of two closed curves, which are mirror images of each other. Their projection in the xy-plane are circles of radius r .

Each part of the intersection can be parametrized by an angle ϕ :

( x , y , z ) = ( r cos ⁡ ϕ , r sin ⁡ ϕ , ± 2 a ( b + r cos ⁡ ϕ ) ) .

The curves contain the following extreme points:

( − r , 0 , ± R 2 − ( r + a ) 2 ) ; ( 0 , ± r , ± R 2 − ( r − a ) ( r + a ) ) ; ( + r , 0 , ± R 2 − ( r − a ) 2 ) .

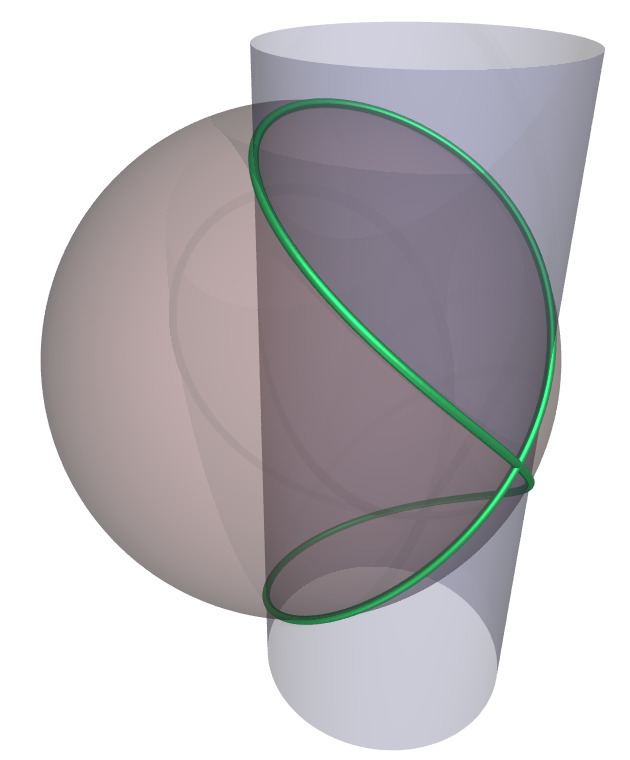
Intersection is a single closed curve

If R < r + a , the intersection of sphere and cylinder consists of a single closed curve. It can be described by the same parameter equation as in the previous section, but the angle ϕ must be restricted to − ϕ 0 < ϕ < + ϕ 0 , where cos ⁡ ϕ 0 = − b / r .

The curve contains the following extreme points:

( − b , ± r 2 − b 2 , 0 ) ; ( 0 , ± r , ± R 2 − ( r − a ) ( r + a ) ) ; ( + r , 0 , ± R 2 − ( r − a ) 2 ) .

Limiting case

In the case R = r + a , the cylinder and sphere are tangential to each other at point ( r , 0 , 0 ) . The intersection resembles a figure eight: it is a closed curve which intersects itself. The above parametrization becomes

( x , y , z ) = ( r cos ⁡ ϕ , r sin ⁡ ϕ , 2 a r cos ⁡ ϕ 2 ) ,

where ϕ now goes through two full revolutions.

In the special case a = r , R = 2 r , the intersection is known as Viviani's curve. Its parameter representation is

( x , y , z ) = ( r cos ⁡ ϕ , r sin ⁡ ϕ , R cos ⁡ ϕ 2 ) .

References

Sphere–cylinder intersection Wikipedia

(Text) CC BY-SA

Contents