 | ||
Introduction
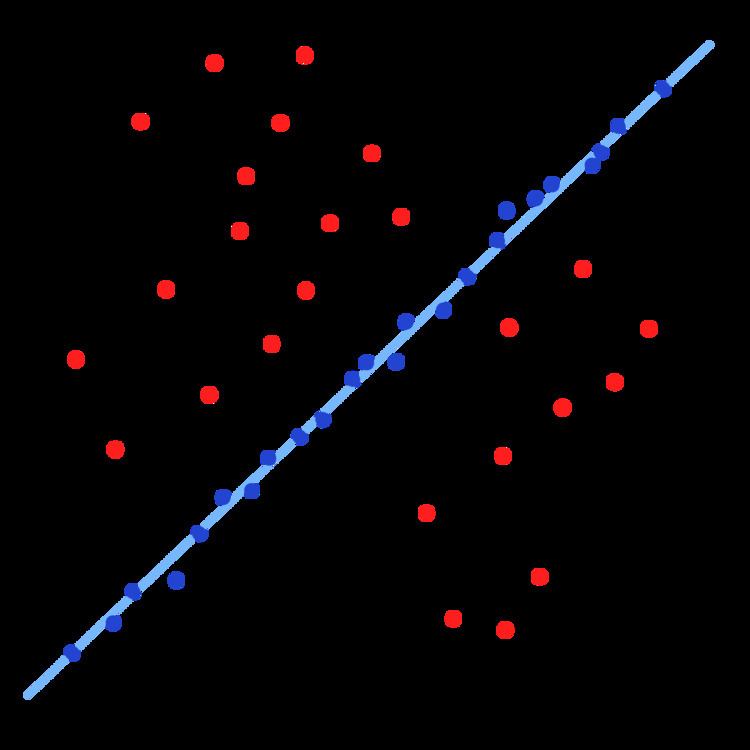
The spatial verification consists in verify a spatial correlation between certain points of a pair of images.
Contents
- Introduction
- Advantages
- Disadvantages
- Methods
- RANSAC Random Sample Consensus
- GHT Generalized Hough Transform
- Examples
- References
The main problem is that outliers (that does not fit or does not match the selected model) affect adjustment called least squares (numerical analysis technique framed in mathematical optimization, which, given an set of ordered pairs: independent variable, dependent variable, and a family of functions, try to find the continuous function).
Advantages
Disadvantages
Methods
The most widely used for spatial verification and avoid errors caused by these outliers methods are:
RANSAC (Random Sample Consensus)
Seeks to avoid the impact of outliers, that not fit with the model, so only considers inline which match the model in question. If an outlier is chosen to calculate the current setting, then the resulting line will have little support from the rest of the points. The algorithm that is performed is a loop that performs the following steps:
- Of the entire input data set, takes a subset randomly to estimate the model.
- Compute model subset. The model is estimated with standard linear algorithms.
- Find the matching values of transformation.
- If the error is minimal model, this is accepted, and if the number of correspondences is long enough, the subset of points involved consensus assembly is referred. And it becomes to compute the estimated model in all correspondences.
The goal is to keep the model with the highest number of matches and the main problem is the number of times you have to repeat the process to obtain the best estimate of the model. RANSAC set in advance the number of iterations of the algorithm.
To specify scenes or objects, is commonly used affine transformations to perform the spatial verification.
GHT (Generalized Hough Transform)
This is a technique for detecting shapes in digital images that solves the veracity of space by clusters of points belonging to the model through a voting procedure on a set of parametric figures.
Not all possible combinations comprovar characteristics by adjusting a model for every possible subset, so that the voting technique, in which a vote is stored for each possible line in which each point is used. Then observe what were the lines with the most votes and those are selected.
If we use the local characteristics of scale, rotation and translation invariant, each feature coincidence gives a hypothesis alignment for scaling, translation and orientation of the model in the picture.
One hypothesis generated by a single match can be unreliable, so for each match (match), a vote is done to get a stronger hypothesis in the Hough space. So we have two major phases:
The main disadvantages are:
