 | ||
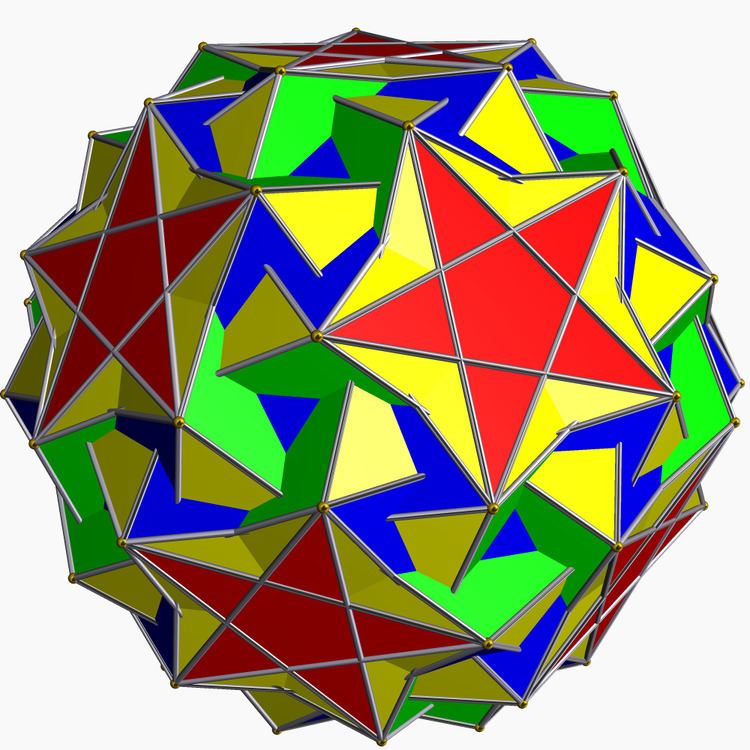
In geometry, the snub icosidodecadodecahedron is a nonconvex uniform polyhedron, indexed as U46.
Contents
Cartesian coordinates
Cartesian coordinates for the vertices of a snub icosidodecadodecahedron are all the even permutations of
(±2α, ±2γ, ±2β),(±(α+β/τ+γτ), ±(-ατ+β+γ/τ), ±(α/τ+βτ-γ)),(±(-α/τ+βτ+γ), ±(-α+β/τ-γτ), ±(ατ+β-γ/τ)),(±(-α/τ+βτ-γ), ±(α-β/τ-γτ), ±(ατ+β+γ/τ)) and(±(α+β/τ-γτ), ±(ατ-β+γ/τ), ±(α/τ+βτ+γ)),with an even number of plus signs, where
α = ρ+1,β = τ2ρ2+τ2ρ+τ,γ = ρ2+τρ,and where τ = (1+√5)/2 is the golden mean and ρ is the real solution to ρ3=ρ+1, or approximately 1.3247180. ρ is called the plastic constant. Taking the odd permutations of the above coordinates with an odd number of plus signs gives another form, the enantiomorph of the other one.
Medial hexagonal hexecontahedron
The medial hexagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform snub icosidodecadodecahedron.
References
Snub icosidodecadodecahedron Wikipedia(Text) CC BY-SA
