Six rays model

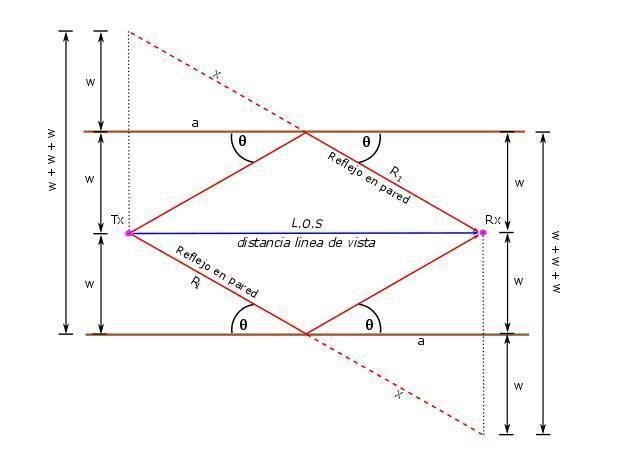
Analysis for antennas of heights equal located in the center of the street

Considering that the height has no variation in the antennas then h t = h r = h , so determines that for the next two rays that are reflected in an occasion in the wall, the point in the which hit is equal to that height h . Likewise for each ray that reflects in the wall exists other ray reflected in the floor in a number equal at the reflections in the wall more one, in such rays exist distances diagonals for each reflect and the total amount of such distances is called d ′

To be located in the center of the street the distance between the antennas T X , R X and the buildings to the width of the streets are equal in both sides so that w t 1 = w r 1 = w t 2 = w r 2 , defining thus an only distance w ..

The mathematical model of propagation of six rays is based in the model of two rays, for find the equation of each ray involved. The distance d that separates the two antennas, is equal to the first ray direct R 0 or line of sight (LOS), that is to say:

R 0 = d

For the ray reflected for below of this R 0 Pythagoras’s theorem applies, in the right triangle formed in the reflection of R 0 as hypotenuse and the ray direct, getting:

R 0 = d 2 + ( 2 h ) 2

For R 1 It is reapplied Pythagoras’s theorem, but knowing that one of the hicks is the double of the distances between the transmitter and the building due to the reflection of w and the distance diagonal to the wall:

R 0 ′ = d 2 + ( 2 w ) 2

For R 1 multiply twice the second ray but it is considered that the distance is the half the third ray for to form the triangle equivalent given that d 1 , is the half of the distance of R 1 must be the half of the distance of line of sight d :

R 1 ′ = 2 ∗ ( R 1 2 ) 2 + ( 2 h ) 2

For R 1 y R 2 the deduction y the distances are equals, therefore:

R 2 = R 1

R 2 ′ = R 1 ′

Analysis for antennas of heights equal located in any point of the street

Due that the direct ray LOS has no changes and doesn't present angular variation between the rays, the distance of the two first rays R 0 and R 0 ′ of model without changes and is deduced according the mathematic model for two rays. For the four rays remaining applies the next mathematical procedure:

R 1 is obtained the next equation through of the analysis geometry of the top view of the model and applies the Pythagoras’s theorem in the triangles, given that the distances between the wall and the antennas w t 1 , w r 1 , w t 2 , w r 2 are different:

R 1 = d 2 − ( w r 2 − w t 2 ) 2 + ( w r 2 + w r 2 ) 2

For similarities of triangles in the top view the model it determined the equation of R 1 :

d ′ = d 2 − ( w r 2 − w t 2 ) 2

a d ′ = w r 2 w t 2 + w r 2 a = d ′ w r 2 ( w t 2 + w r 2 )

x = ( w t 2 ) 2 + a 2 y = R 1 − x

R 1 ′ = x 2 + ( 2 h ) 2 + y 2 + ( 2 h ) 2

For R 1 y R 2 the deduction y the distances are equal therefore:

R 2 = R 1

R 2 ′ = R 1 ′

Analysis for antennas of heights different located in the center of the street

For antennas of different heights with rays that rebound in the wall, observed that the wall is the half point, where the two transmitted rays they fall on such wall. This wall has half the height between the height of the T X and R X smaller than the transmitter and higher than the receiver and this high is where the two rays impact in the point, then rebound to the receiver. The ray reflected leaves two reflections, one that it has the same high of the wall and the other the receiver, and the ray of the line of sight maintains the same direction between the T X and the R X The diagonal distance d´ that separates the two antennas divides in two distances through of the wall, one is called a and the other d − a .

Analysis for antennas of heights different located in any point of the street

For the mathematical six rays model of propagation for antennas of different heighs located in any point of the street, is based on the model of the two rays to find the equations of each ray involved in this model, each antenna has a different height, then h t ≠ h r , there a direct distance d that separates the two antennas, the first ray is formed applying Pythagoras’s theorem since the difference of heights of the antennas with respect to line of sight:

R 0 = d 2 + ( h t − h r ) 2

The second ray or the reflected ray does similar to the first ray but adds the heights of the antennas to form the right triangle for the reflection of the heigh of the transmitter :

R 0 ′ = d 2 + ( h t + h r ) 2

For deducing the third ray it is found that angle between the direct distance d and the distance of line of sight R 0

cos ⁡ θ = h t − h r R 0

Now deducing the height that subtraction of the wall with respect the height of the receiver called z by similarity the triangles:

z a = h t d ′ z = h t   a d ′

By similarity of triangles it can be deduced the distance where the ray hits the wall until the perpendicular of the receiver called a achieved:

a w t 2 = d ′ w t 1 + w r 1 a = d ′ w t 2 ( w t 1 + w r 1 )

R 1 = ( h t − h r − z ) 2 + ( d ′ − a ) 2 + z 2 + a 2 cos ⁡ θ

By similarity of the triangles can be deduced the equation of the fourth ray, observing:

R 1 ′ = ( h t + h r + z ) 2 + ( d ′ − a ) 2 + ( 2 h r + z ) 2 + a 2 cos ⁡ θ

For R 1 y R 2 the deduction and the distances are equal, therefore:

R 2 = R 1

R 2 ′ = R 1 ′

Losses for trajectory on free space

Considering a transmitted signal through of the free space to a receiver located at a distance d of the transmitter.Assuming that there is no obstacle between the transmitter and the receiver, the signal it spreads along of a straight line between the two. The model of ray associated with this transmission is called line of sight (LOS), and the signal receives corresponding is called signal of LOS

The loss of trajectory on free space of the model of six ray in the space free is defined as:

p 0 ( t ) = ( G i G R ) λ 4 π ( exp ⁡ ( j ∗ 2 π ∗ R 0 / λ ) R 0 + Γ exp ⁡ ( j ∗ 2 π ∗ R 0 ′ / λ ) R 0 ′ )

p 1 ( t ) = ( G i G R ) λ 4 π   Γ 1 ( exp ⁡ ( j ∗ 2 π ∗ R 1 / λ ) R 1 + Γ exp ⁡ ( j ∗ 2 π ∗ R 1 ′ / λ ) R 1 ′ )

p 2 ( t ) = ( G i G R ) λ 4 π   Γ 1 ( exp ⁡ ( j ∗ 2 π ∗ R 2 / λ ) R 2 + Γ exp ⁡ ( j ∗ 2 π ∗ R 2 ′ / λ ) R 2 ′ )

P L   ( d B ) = 20 log ⁡ |   ∑ i = 0 N P i   |