 | ||
In the mathematical field of algebraic geometry, a singular point of an algebraic variety V is a point P that is 'special' (so, singular), in the geometric sense that at this point the tangent space at the variety may not be regularly defined. In case of varieties defined over the reals, this notion generalizes the notion of non-local flatness. A point of an algebraic variety which is not singular is said to be regular. An algebraic variety which has no singular point is said to be non singular or smooth.
Contents
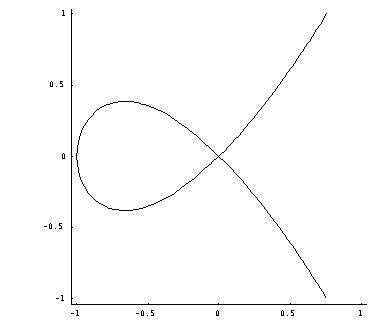
For example, the plane algebraic curve (a cubic curve) of equation
y2 - x2(x + 1) = 0,which is plotted below, crosses itself at the origin (0,0) and the origin is thus a double point of the curve. It is singular because a single tangent may not be correctly defined there.
More generally a plane curve defined by an implicit equation
F(x,y) = 0,where F is a smooth function is said to be singular at point if the Taylor series of F has order at least 2 at this point.
The reason for that is that, in differential calculus, the tangent at the point (x0, y0) of such a curve is defined by the equation
whose left-hand side is the term of degree one of the Taylor expansion. Thus, if this term is zero, the tangent may not be defined in the standard way, either because it does not exists or a special definition must be provided.
In general for a hypersurface
F(x, y, z, ...) = 0the singular points are those at which all the partial derivatives simultaneously vanish. A general algebraic variety V being defined as the common zeros of several polynomials, the condition on a point P of V to be singular point is that the Jacobian matrix of the first order partial derivatives of the polynomials has a rank at P that is lower than the rank at other points of the variety.
Points of V that are not singular are called non-singular or regular. It is always true that almost all points are non-singular, in the sense that the non-singular points form a set that is both open and dense in the variety (for the Zariski topology, as well as, in the case of varieties defined over the complexes, for the usual topology).
In case of a real variety (that is the set of the points with real coordinates of a variety defined by polynomials with real coefficients), the variety is a manifold near every regular point. But it is important to note that a real variety may be a manifold and have singular points. For example the equation
Singular points of smooth mappings
As the notion of singular points is a purely local property, the above definition can be extended to cover the wider class of smooth mappings, (functions from M to Rn where all derivatives exist). Analysis of these singular points can be reduced to the algebraic variety case by considering the jets of the mapping. The k-th jet is the Taylor series of the mapping truncated at degree k and deleting the constant term.
Nodes
In classical algebraic geometry, certain special singular points were also called nodes. A node is a singular point where the Hessian matrix is non-singular; this implies that the singular point has multiplicity two and the tangent cone is not singular outside its vertex.
