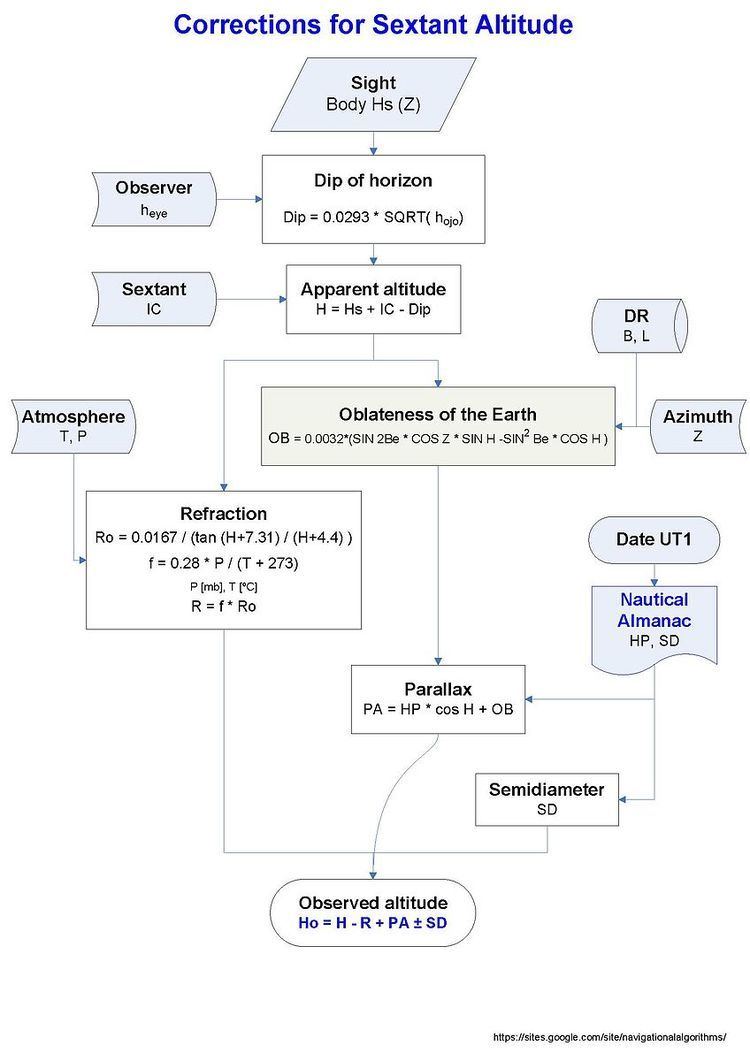
 | ||
Sight reduction is the process of deriving from a sight the information needed for establishing a line of position.
Contents
- Tabular sight reduction
- Longhand haversine sight reduction
- Doniol
- Ultra compact sight reduction
- An example
- References
Sight is defined as the observation of the altitude, and sometimes also the azimuth, of a celestial body for a line of position; or the data obtained by such observation.
Nowadays sight reduction uses the equation of the circle of equal altitude to calculate the altitude of the celestial body,
and the azimuth Zn is obtained from Z by:
With the observed altitude Ho, Hc and Zn are the parameters of the Marcq St Hilaire intercept for the line of position:
With B the latitude (+N/S), L the longitude (+E/-W), LHA = GHA + L is the local hour angle, Dec and GHA are the declination and Greenwich hour angle of the star observed, and Hc the calculated altitude. Z is the calculated azimuth of the body.
Basic procedures involved computer sight reduction or longhand tabular methods.
Tabular sight reduction
The methods included are:
Longhand haversine sight reduction
This method is a practical procedure to reduce celestial sights with the needed accuracy, without using electronic tools such as calculator or a computer. And it could serve as a backup in case of malfunction of the positioning system aboard.
Doniol
The first approach of a compact and concise method was published by R. Doniol in 1955 The altitude is derived from sin(Hc) = n − a (m + n), in which n = cos(B − Dec), m = cos(B + Dec), a = hav(LHA).
The calculation is:
n = cos(B - Dec)m = cos(B + Dec)a = hav(LHA)sin_Hc = n - a (m + n)Hc = arcsin(sin_Hc)Ultra compact sight reduction
A practical and friendly method using haversines was developed between 2014 and 2015, and published in NavList.
A compact expression for the altitude was derived using haversines, hav, for all the terms of the equation:
hav(ZD) = hav(B - Dec) + (1 - hav(B - Dec) − hav(B + Dec)) hav(LHA)
where ZD is the zenith distance
Hc = (90 - ZD) the calculated altitude
The algorithm if absolute values are used is:
if same name for latitude and declination n = hav(|B| - |Dec|) m = hav(|B| + |Dec|)if contrary name n = hav(|B| + |Dec|) m = hav(|B| - |Dec|)q = n + ma = hav(LHA)hav(ZD) = n + (1 - q) aZD = invhav -> look at the haversine tablesHc = 90° - ZDFor the azimuth a diagram was developed for a faster solution without calculation, and with an accuracy of 1°.
This diagram could be used also for star identification.
An ambiguity in the value of azimuth may arise since in the diagram 0 ≤ Z ≤ 90°. Z is E/W as the name of the meridian angle, but the N/S name is not determined. In most situations azimuth ambiguities are resolved simply by observation.
When there are reasons for doubt or for the purpose of checking the following formula should be used.
hav(Z) = [hav(90° - Dec) - hav(B - Hc)] / (1 - hav(B - Hc) - hav(B + Hc))
The algorithm if absolute values are used is:
if same name a = hav(90° - |Dec|)if contrary name a = hav(90° + |Dec|)m = hav(B + Hc)n = hav(B - Hc)q = n + mhav(Z) = (a - n) / (1 - q)Z = invhav -> look at the haversine tablesif Latitude N: if LHA > 180°, Zn = Z if LHA < 180°, Zn = 360° − Zif Latitude S: if LHA > 180°, Zn = 180° − Z if LHA < 180°, Zn = 180° + ZThis computation of the altitude and the azimuth needs a haversine table. For a precision of 1 minute of arc, a four figure table is enough.
