 | ||
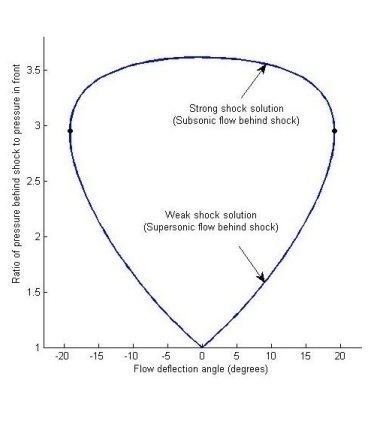
The term shock polar is generally used with the graphical representation of the Rankine-Hugoniot equations in either the hodograph plane or the pressure ratio-flow deflection angle plane. The polar itself is the locus of all possible states after an oblique shock.
Contents
Shock Polar in the ( φ , p ) {\displaystyle (\varphi ,p)} Plane
The minimum angle,
To calculate the possible flow deflection angles, the relationship between shock angle
Where
Uses of Shock Polars
One of the primary uses of shock polars is in the field of shock wave reflection. A shock polar is plotted for the conditions before the incident shock, and a second shock polar is plotted for the conditions behind the shock, with its origin located on the first polar, at the angle through which the incident shock wave deflects the flow. Based on the intersections between the incident shock polar and the reflected shock polar, conclusions as to which reflection patterns are possible may be drawn. Often, it is used to graphically determine whether regular shock reflection is possible, or whether Mach reflection occurs.
