Shear mapping - Alchetron, The Free Social Encyclopedia

In plane geometry, a shear mapping is a linear map that displaces each point in fixed direction, by an amount proportional to its signed distance from a line that is parallel to that direction. This type of mapping is also called shear transformation, transvection, or just shearing.

An example is the mapping that takes any point with coordinates ( x , y ) to the point ( x + 2 y , y ) . In this case, the displacement is horizontal, the fixed line is the x -axis, and the signed distance is the y coordinate. Note that points on opposite sides of the reference line are displaced in opposite directions.

Shear mappings must not be confused with rotations. Applying a shear map to a set of points of the plane will change all angles between them (except straight angles), and the length of any line segment that is not parallel to the direction of displacement. Therefore it will usually distort the shape of a geometric figure, for example turning squares into non-square parallelograms, and circles into ellipses. However a shearing does preserve the area of geometric figures and the alignment and relative distances of collinear points. A shear mapping is the main difference between the upright and slanted (or italic) styles of letters.

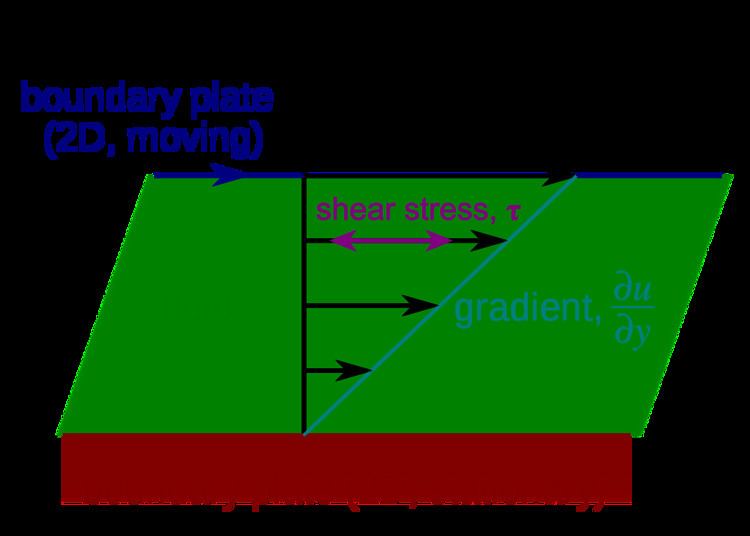
The same definition is used in three-dimensional geometry, except that the distance is measured from a fixed plane. A three-dimensional shearing transformation preserves the volume of solid figures, but changes areas of plane figures (except those that are parallel to the displacement). This transformation is used to describe laminar flow of a fluid between plates, one moving in a plane above and parallel to the first.

In the general n -dimensional Cartesian space R n , the distance is measured from a fixed hyperplane parallel to the direction of displacement. This geometric transformation is a linear transformation of R n that preserves the n -dimensional measure (hypervolume) of any set.

Horizontal and vertical shear of the plane

In the plane R 2 = R × R , a horizontal shear (or shear parallel to the x axis) is a function that takes a generic point with coordinates ( x , y ) to the point ( x + m y , y ) ; where m is a fixed parameter, called the shear factor.

The effect of this mapping is to displace every point horizontally by an amount proportionally to its y coordinate. Any point above the x -axis is displaced to the right (increasing x ) if m > 0 , and to the left if m < 0 . Points below the x -axis move in the opposite direction, while points on the axis stay fixed.

Straight lines parallel to the x -axis remain where they are, while all other lines are turned, by various angles, about the point where they cross the x -axis. Vertical lines, in particular, become oblique lines with slope 1 / m . Therefore the shear factor m is the cotangent of the angle φ by which the vertical lines tilt, called the shear angle.

If the coordinates of a point are written as a column vector (a 2×1 matrix), the shear mapping can be written as multiplication by a 2×2 matrix:

( x ′ y ′ ) = ( x + m y y ) = ( 1 m 0 1 ) ( x y ) .

A vertical shear (or shear parallel to the y -axis) of lines is similar, except that the roles of x and y are swapped. It corresponds to multiplying the coordinate vector by the transposed matrix:

( x ′ y ′ ) = ( x m x + y ) = ( 1 0 m 1 ) ( x y ) .

The vertical shear displaces points to the right of the y -axis up or down, depending on the sign of m . It leaves vertical lines invariant, but tilts all other lines about the point where they meet the y -axis. Horizontal lines, in particular, get tilted by the shear angle φ to become lines with slope m .

General shear mappings

For a vector space V and subspace W, a shear fixing W translates all vectors parallel to W.

To be more precise, if V is the direct sum of W and W′, and we write vectors as

v = w + w′

correspondingly, the typical shear fixing W is L where

L(v) = (w + Mw′) + w ′

where M is a linear mapping from W′ into W. Therefore in block matrix terms L can be represented as

( I M 0 I )

Applications

The following applications of shear mapping were noted by William Kingdon Clifford:

"A succession of shears will enable us to reduce any figure bounded by straight lines to a triangle of equal area.""... we may shear any triangle into a right-angled triangle, and this will not alter its area. Thus the area of any triangle is half the area of the rectangle on the same base and with height equal to the perpendicular on the base from the opposite angle."

The area-preserving property of a shear mapping can be used for results involving area. For instance, the Pythagorean theorem has been illustrated with shear mapping.

An algorithm due to Alan W. Paeth uses a sequence of three shear mappings (horizontal, vertical, then horizontal again) to rotate a digital image by an arbitrary angle. The algorithm is very simple to implement, and very efficient, since each step processes only one column or one row of pixels at a time.

The italics text can be thought of as normal text under a shear.

References

Shear mapping Wikipedia

(Text) CC BY-SA

Contents

Horizontal and vertical shear of the plane

General shear mappings

Applications

References