 | ||
A column can buckle due to its own weight with no other direct forces acting on it, in a failure mode called self-buckling. In conventional column buckling problems, the self-weight is often neglected since it is assumed to be small when compared to the applied axial loads. However, when this assumption is not valid, it is important to take the self-buckling into account.
Elastic buckling of a "heavy" column i.e., column buckling under its own weight, was first investigated by Greenhill at 1881. He found that a free-standing, vertical column, with density
where
One interesting example for the use of the equation was suggested by Greenhill in his paper. He estimated the maximal height of a pine tree, and found it cannot grow over 90 ft tall. This length sets the maximum height for trees on earth if we assume the trees to be prismatic and the branches are neglected.
Mathematical Derivation
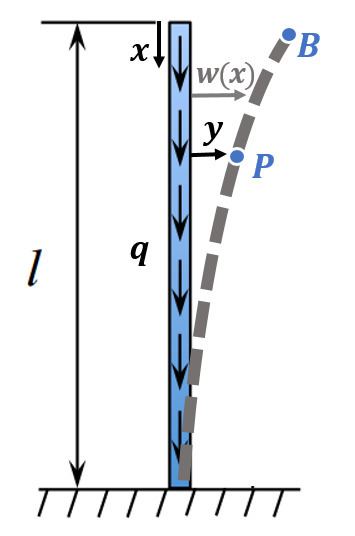
Suppose a uniform column fixed in a vertical direction at its lowest point, and carried to a height
The column is slightly curved under its own weight, so the curve
Looking at any point on the column, we can write the moment equilibrium:
where the right-hand side of the equation is the moment of the weight of BP about P.
According to Euler–Bernoulli beam theory:
Where
Therefore, the differential equation of the central line of BP is:
Differentiating with respect to x, we get
Or
We get that the governing equation is the third order linear differential equation with a variable coefficient. The way to solve the problem is to use new variables
Then, the equation transforms to the Bessel equation
The solution of the transformed equation is
Where
Now, we will use the boundary conditions:
From the second B.C., we get that the critical length in which a vertical column will buckle under its own weight is:
Using
